Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Polinomioen grafikoak

Author:Izar Azpiroz, AdelaTavacova

3.mailako polinomioak

Grafikoak honako polinomioa bisualizatzen du: . Aztertu koefizienteen aldaketak nola eragiten duen grafikoan.

Leading coefficient

Describe how the value of affects the graph of a third-degree polynomial.

Constant coefficient

What point does the coefficient represent on the graph?

Check my answer
As you are changing the coefficients, the graph of a third-degree polynomial is also changing. However, there are certain patterns that can be generalized for all third degree polynomials. Use the applet to describe possible cases of graphs and answer the following questions.

Zeros (x-intercepts)

How many zeros can a third-degree polynomial have? Consider all possible cases.

Select all that apply
  • A
  • B
  • C
  • D
  • E
Check my answer (3)

Turning points and terrace points

Turning points and terrace points

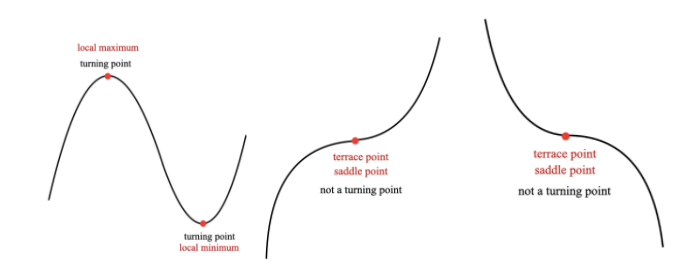
Turning points

What is the MAXIMUM NUMBER of turning points that a third-degree polynomial can have? (Turning point: local minimum or local maximum)

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Terrace points

What is the MAXIMUM number of TERRACE POINTS that a third-degree polynomial can have?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

FOURTH-DEGREE POLYNOMIALS

You will now be investigating graphs of fourth-degree polynomials. Read the tip about working with the sliders.

Zeros

How many zeros can a fourth-degree polynomial have?

Select all that apply
  • A
  • B
  • C
  • D
  • E
  • F
Check my answer (3)

Turning points

What is the MAXIMUM NUMBER of turning points that a fourth-degree polynomial can have? (Turning point: local minimum or local maximum)

Select all that apply
  • A
  • B
  • C
  • D
  • E
Check my answer (3)

Terrace points

What is the MAXIMUM number of terrace points that a fourth-degree polynomial can have?

Select all that apply
  • A
  • B
  • C
  • D
  • E
Check my answer (3)

Higher-degree polynomials

The following applet allows you to analyze also some higher degree polynomials. Your goal is to derive a general rule about the number of zeros and turning points of an n-th degree polynomial - see statements below.

GENERAL RULE about the number of ZEROS of a polynomial of n-th degree.

Complete the statement: Polynomials of degree have at most ......... real zeros.

Check my answer

GENERAL RULE about the number of TURNING POINTS of a polynomial of n-th degree.

Complete the statement. Polynomials of degree have at most ....... turning points.

Check my answer

New Resources

Discover Resources

Discover Topics