Integral Definida
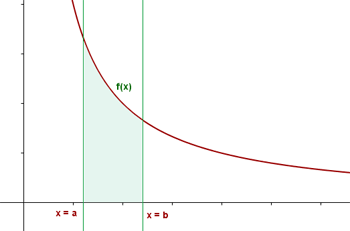
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.
- La integral definida se representa por
 .
. - ∫ es el signo de integración.
- a límite inferior de la integración.
- b límite superior de la integración.
- f(x) es el integrando o función a integrar.
- dx es diferencial de x, e indica cuál es la variable de la función que se integra.
En este applet se muestra la gráfica de la función f(x)=x/(x²+1) en color naranja. En color azul la función que representa la integral indefinida de f(x). Si usted mueve los parámetros “a” y “b” ubicados en el extemo superior izquierdo, podrá percatarse que se obtiene la integral definida en la fila 1 del CAS (pantalla de en medio) para el intervalo [a,b]. El parámetro “n” corresponde a la cantidad de rectágulos que se desea elaborar. En las filas 2 y 3 se obtienen las sumas inferior y superior de f(x), para ese mismo intervalo. Y en la fila 4 se obtiene el promedio de las sumas, solicitando se compare este valor con el obtenido en la fila 1, que corresponde al de la integral indefinida. ¿Qué conclusiones obtiene?
Ahora te invitamos a que observes el siguiente video, para penetrar más en el mundo de las integrales definidas.Integrales
Fuentes de Consulta:
El Traductor de ingeniería. (17 de Enero de 2020). Obtenido de https://www.youtube.com/watch?v=Ec-cGjh0Fr0
Super profe. (17 de Enero de 2020). Obtenido de https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/integral-definida.html