6.Obtención de las ecuaciones de un plano
Obtención de la ecuaciones de un plano dados un punto y un plano paralelo.
Se tiene la ecuación de un plano Ax+By+Cz=d, cuando "d" sea cero, esto quiere decir que ese plano pasa por el origen y puede escribirse como Ax+By+Cz=0.
Para encontrar la ecuación de un plano paralelo a Ax+By+Cz=0 cuando se tiene un punto Q=(x1, y1, z1), tenemos que sustituir x, y, z en la ecuación.
Cuando se realiza la operación podemos obtener el nuevo "d" para la ecuación del plano paralelo al primero y podemos escribir la ecuación del mismo.
Ejemplo:
Sea P dado por 8x − 6y + 7z = −12. Encontrar la ecuación del plano que es paralelo a P y que pasa por:
(a)El origen (b) Q = (1, -2, 3)
SOLUCION:
Como cualquier plano tiene un punto que pasa por el origen, podemos decir que d seria igual a 0.
Igualando la ecuación del plano a 0:
Sustituyendo las coordenadas dadas con x, y, z:
Ya que se obtuvo el valor "d" para el plano paralelo al primero, lo sustituimos en el "d" de la ecuación y tenemos la ecuación del nuevo plano.
Problema
Encuentre la ecuación del plano que es paralelo a 3x+6y+z=-48 y que pasa por el punto Q=(8, 5, 2).
Observaciones
Podemos notar como un plano tiene una infinidad de planos paralelos y estos varían conforme el valor de un punto en ellos, el cual nos puede ayudar a definir el valor "d" en cada ecuación de cada plano paralelo.
Obtención de las ecuaciones de un plano dados un punto y dos planos perpendiculares.
Tenemos dos ecuaciones de los planos perpendiculares, sea y ,
también contamos con un punto , para poder encontrar el plano que pasa por el punto Q y es perpendicular a los otros dos planos, es necesario conocer otros dos puntos derivados de las ecuaciones de los planos conocidos.
y
Consideramos a R y S como vectores normales y podemos, siempre que R y S no sean combinación lineal para asegurar que son perpendiculares.
y
Posteriormente realizamos un producto vectorial para poder encontrar la ecuación del plano perpendicular.
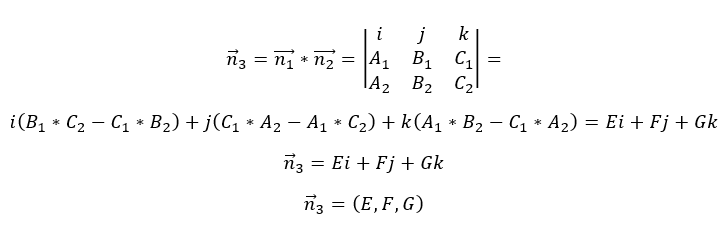
Finalmente encontramos la ecuación del tercer plano, usamos la formula general del plano ya que y .
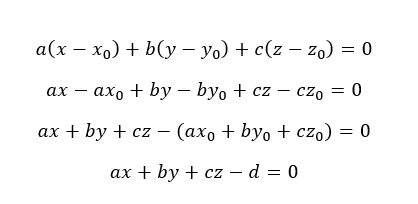
Nota
Como paso final, se multiplica toda la ecuación por (-1) y se divide entre 2.
EJEMPLO:


Ejemplo grafico.
Podemos observar que solo existen ciertos puntos en el espacio para que se encuentre el tercer plano, como en este caso donde se considera a P=(3,-1,0)