Voorbeeld + opgaven 15 en 16
Voorbeeld
Gegeven is de functie f met voorschrift f(x) = 4−x2.
Bereken het differentiequotiënt op het interval [0,2] en beschrijf de betekenis van dit getal.
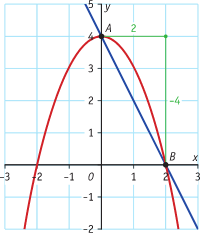
Oplossing:
Het differentiequotiënt is het hellingsgetal van het lijnstuk AB. Het is de gemiddelde verandering van de functiewaarden op het interval [0,2]. Het geeft de toename of de afname van f(x) per eenheid van x weer.
Opgave 15
Gegeven is de functie f(x) = (x−2)2+3.
a. Bereken het differentiequotiënt op het interval [1,5].
b. Bereken het differentiequotiënt van f op het interval [-2,4] . Rond je antwoord af op één decimaal.
Opgave 16
Gegeven is de functie f(x) = x3−5x+4.
a. Bereken het differentiequotiënt op het interval [-5,5].
b. Maak met de grafische rekenmachine een tabel met stapgrootte 1 van de formule en zoek een interval waarop de gemiddelde verandering gelijk is aan 16 .