RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO QUALQUER
PROCEDIMENTOS:
Por meio de questionamento apresentar as relações métricas em um triângulo retângulo qualquer.
Questão 1
Usando a semelhança de t1 e t2 tem-se: b/n1= a/b1 b/n= a/b. O resultado pode ser expresso por?
Questão 2
Utilizando a semelhança de t1 e t3 tem-se: c/m1= a/c1 c/m= a/c. O resultado será expresso como?
Questão 3
Adicionar membro a membro as igualdades das expressões: b2= am e c2 = na e efetuar as substituições necessárias. O resultado gerará que expressão?
TEOREMA DE PITÁGORAS
APRESENTAÇÃO:
A indução da fórmula: a2= b2 + c2 como sendo da demonstração do Teorema atribuído a Pitágoras ou a Escola Pitagórica, porém existem evidências da aplicação deste teorema anteriores à existência de Pitágoras.
A variante desta fórmula em termos de geometria é representada pela construção:
Questão 4
Aplicar o a semelhançade t1 e t3 induzir, respectivamente, as relações métricas em um triângulo retângulo: cm= bh e ch=bn.
SUGESTÃO DESAFIADORA:
Empregando as relações métricas em um triângulo retângulo e os procedimentos propostos e observar a imagem do triângulo retângulo a seguir:
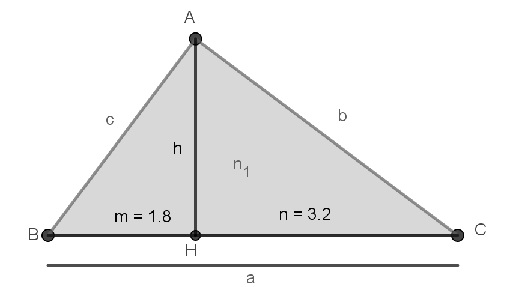
PENSAR E RESOLVER
Determinar as medidas dos elementos do elementos do triângulo ABC: a, b, c e h.
ARREMATE
Pode-se asseverar que ao traçar a altura em um triângulo retângulo qualquer relativa à hipotenusa
divide-se o triângulo original em dois outros triângulos retângulos que são semelhantes ao original e pelo princípio da transitividade semelhantes entre si.