Interpolación polinómica a trozos

Una herramienta muy eficiente para interpolar una serie de puntos determinados , es en lugar de crear un solo polinomio que interpole todos los puntos, crear una serie de ecuaciones más sencillas que interpolen a cada par de puntos consecutivos , para . Ésta es la idea base de la función spline la cual definiremos a continuación.

Suponga que tenemos una serie de puntos donde las abcisas no son necesariamente equidistantes, pero si convenientemente ordenadas de forma que <<<, entonces diremos que una función spline de grado , es una función que cumple

1. para toda
2. es un polinomio de grado en cada subintervalo
3. tiene una derivada continua hasta de orden en

Por ejemplo, dados puntos , una spline de grado o lineal, sería aquella cuya gráfica la forman rectas a trozos, es decir segmentos sobre una partición << del intervalo , de tal manera que el extremo final de un segmento coincide con el principio del siguiente.

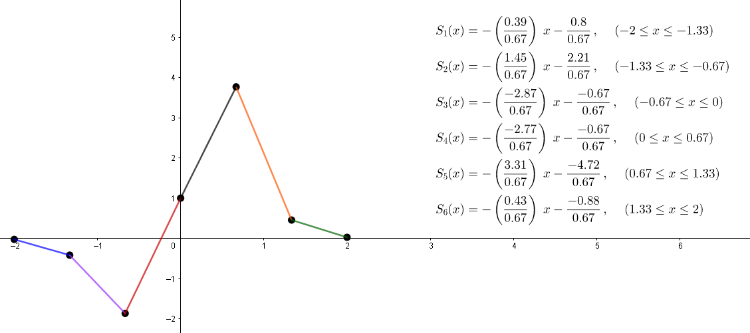
La spline cumple su objetivo al interpolar los puntos dados, sin embargo, las ecuaciones que definen a la spline, son rectas que carecen de suavidad. Se requiere entonces una spline de grado mayor que pueda interpolar dichos puntos. La spline necesaria que interpola los puntos dados, que es lo suficientemente suave y que entre todas resulta la más adecuada, es la de grado o cúbica. Observemos la siguiente spline cúbica que interpola los puntos mencionados anteriormente

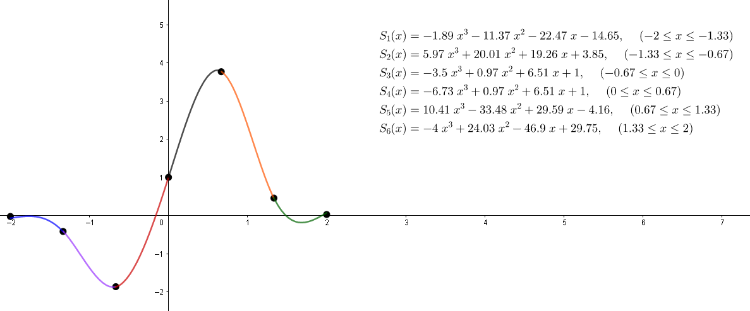
Observemos que las ecuaciones que definen la spline cúbica, son curvas suaves que se conectan entré sí en los puntos dados. Además, la elección de la spline cúbica, minimiza las oscilaciones de las curvas entre los puntos a interpolar (Chica, 2018) tal como lo podemos ver en el siguiente applet

Las propiedades y construcción de la spline cúbica, será nuestro objeto de estudio a continuación.