Concavidade e os pontos de inflexão
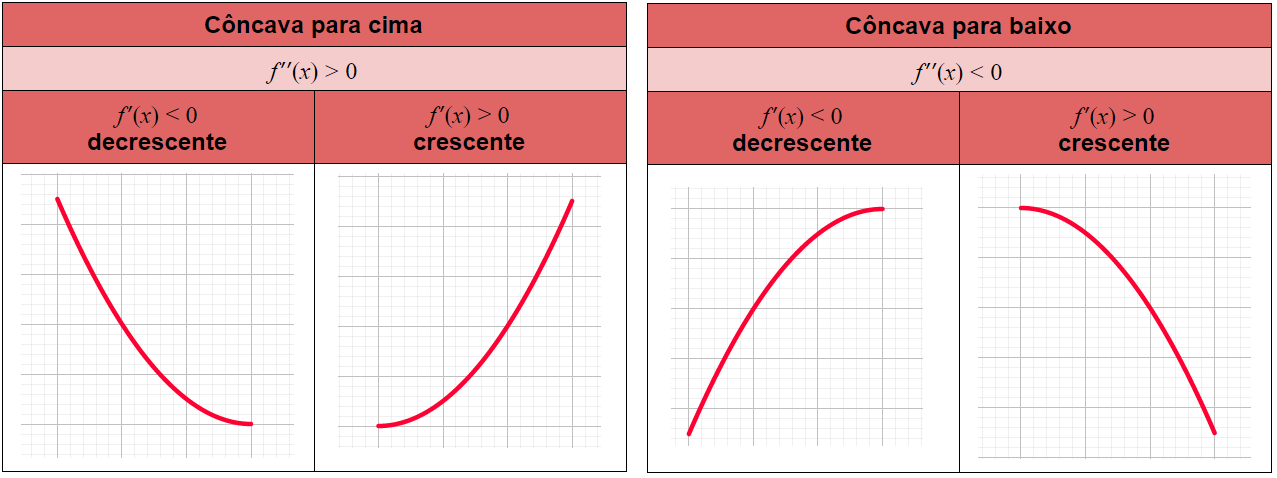
Definção
Seja uma função contínua em e diferenciável em e .
tem um ponto de inflexão em , se troca de concavidade em .
Corolário:
Seja uma função contínua em e duas vezes diferenciável em e um ponto crítico ().
é um ponto de inflexão se e somente se troca de sinal em .