Sucesiones
Sucesión: Una sucesión es una función definida de que se acostumbra a denotar por en lugar de , así:
: se llama término n-ésimo o término de lugar n.
: es el primer término de la sucesión.
: es el k-ésimo término de la sucesión.
Términos de una sucesión: Dada la sucesión , … , , su k–ésimo término es , el
siguiente término es también llamado sucesor, el anterior al k–ésimo término es
también llamado antecesor.
Formación de una sucesión: las sucesiones se pueden representar a través de un término
general, o bien de manera recursiva. Ambos conceptos representan de manera clara el
comportamiento de la sucesión, pero es mucho mejor solo tener una expresión que dependa de
la posición en la que me encuentro, más que de su término anterior.
Representación gráfica de una sucesión: Las sucesiones se pueden representar de manera
gráfica en los reales, ya que son funciones de los naturales a los reales. Por lo que podemos
realizar una gráfica de la sucesión. Por ejemplo, sea la sucesión anterior, entonces
su grafica será de la siguiente manera.
Monotonía de una sucesión:

Obsérvese que la única diferencia entre sucesión creciente y estrictamente creciente es que en
la segunda la desigualdad debe cumplirse necesariamente mientras que en las crecientes puede
haber igualdad entre términos sucesivos.
Una sucesión {} es monótona decreciente si:
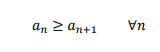

Convergencia de una sucesión
Estudiar la convergencia de una sucesión consiste en investigar a qué valor tiende el término
genérico de la misma cuando
Si tiende a un número finito la sucesión se dice convergente, si tiende al "∞" o no existe el
número , la sucesión se dice divergente.
Definición formal: Si los valores de se pueden hacer tan cerca como queramos a tomando
valores de suficientemente cerca de ∞ (tan grandes como queramos), entonces escribimos: