4. Véletlen háromszög területe
Egy egységsugarú körön véletlenszerűen választunk három pontot. A valószínűségi változó az általuk meghatározott háromszög területe.
Legyen , , , ahol és ! Ekkor a területfüggvény grafikonja:
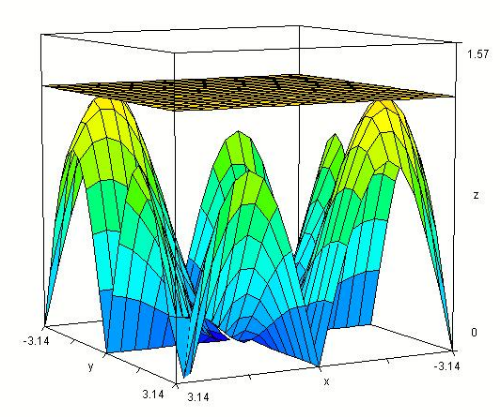
A számolás az alábbi GeoGebra CAS fájlban látható. A vektoriális szorzat fogalmát használtuk.
A kapott területfüggvény hozzárendelési szabálya és grafikonja alapján néhány tulajdonsága megsejthető.
Összefoglalva azt, amit eddig tudunk/sejtünk:
- zérushelyek.
- .
- A függvény értékkészlete: .
- Maximumhelyek: .
Az eloszlásfüggvény értékét megkapjuk úgy, hogy az alábbi ábrán piros színnel jelzett síkrész területét elosztjuk -tel.
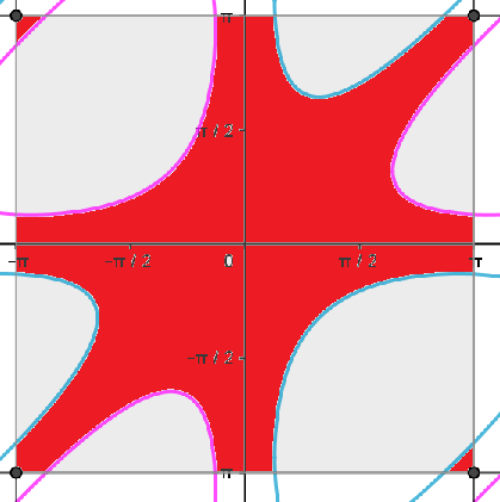
A következő lépés e terület kiszámítása lesz.(?)