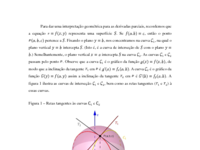
Interpretação geométrica de derivadas parciais

Autor:Raiane Lemke

Sobre a interpretação geométrica de derivadas parciais, Stewart (2010), traz que uma das ideias mais principais em cálculo de funções de uma variável é que “à medida que damos zoom em torno de um ponto no gráfico de uma função diferenciável, esse gráfico vai se tornando indistinguível de sua reta tangente, e podemos aproximar a função por uma função linear. ” (STEWART, 2010, p. 848). Uma ideia semelhante pode ser desenvolvida para o ambiente tridimensional:

À medida que damos zoom em torno de um ponto na sua superfície que é o gráfico de uma função diferenciável de duas variáveis, essa superfície parece mais e mais com um plano (seu plano tangente) e podemos aproximar a função, nas proximidades do ponto, por uma função linear de duas variáveis.(STEWART, 2010, p. 848).

O próprio GeoGebra oferece a ferramenta de zoom. Na figura 0 podemos observar um plano tangente à um paraboloide e dando um zoom no gráfico podemos ver que perto do ponto o paraboloide pode ser aproximado por um plano.