Θεωρία 3
Ανάλογα ποσά
- Δύο ποσά λέγονται ανάλογα, εάν μεταβάλλονται με τέτοιο τρόπο, που όταν οι τιμές του ενός πολλαπλασιάζονται με έναν αριθμό, τότε και οι αντίστοιχες τιμές του άλλου να πολλαπλασιάζονται με τον ίδιο αριθμό.
- Δύο ποσά x και y είναι ανάλογα, όταν οι αντίστοιχες τιμές τους δίνουν πάντα ίδιο πηλίκο:
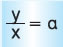. Το πηλίκο α λέγεται συντελεστής αναλογίας.
- Τα ανάλογα ποσά x και y συνδέονται με τη σχέση:
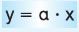όπου α ο συντελεστής αναλογίας. - Όταν το ποσό y είναι ποσοστό του ποσού x, τα δύο ποσά συνδέονται με τη σχέση
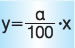και είναι ανάλογα, με συντελεστή αναλογίας το 
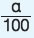ή α%.
- Τα ανάλογα ποσά x και y συνδέονται με τη σχέση:
- Η σχέση y = α · x εκφράζει μια αλληλεπίδραση των ποσών x και y. Συγκεκριμένα, ο διπλασιασμός, τριπλασιασμός κ.ο.κ. του ενός ποσού επιφέρει διπλασιασμό, τριπλασιασμό κ.ο.κ. του άλλου ποσού.
Ιδιότητες ανάλογων ποσών
Δύο ποσά α, γ λέγονται ανάλογα προς δύο άλλα ποσά β, δ όταν
ο λόγος του α προς το β ισούται με το λόγο του γ προς το δ, δηλαδή όταν ισχύει:
Αυτό σημαίνει ότι υπάρχει θετικός αριθμός λ, ώστε να ισχύει α = λ ·β και γ = λ · δ.
Η παραπάνω ισότητα λέγεται αναλογία με όρους τα α, β, γ και δ.
Τα α και β λέγονται ομόλογοι ή αντίστοιχοι όροι. Το ίδιο και τα γ και δ.
Τα α, δ λέγονται άκροι όροι, ενώ τα β, γ μέσοι όροι της αναλογίας.
Ο τέταρτος όρος δ της αναλογίας λέγεται και τέταρτη ανάλογος των α, β και γ.
Σε κάθε αναλογία ισχύουν οι ιδιότητες:
i) το γινόμενο των άκρων ισούται με το γινόμενο των μέσων όρων (τα χιαστί γινόμενα είναι ίσα).
ii) μπορούμε να εναλλάξουμε την θέση των μέσων όρων της. (Ισχύει και για τους άκρους)
Αυτό σημαίνει ότι υπάρχει θετικός αριθμός λ, ώστε να ισχύει α = λ ·β και γ = λ · δ.
Η παραπάνω ισότητα λέγεται αναλογία με όρους τα α, β, γ και δ.
Τα α και β λέγονται ομόλογοι ή αντίστοιχοι όροι. Το ίδιο και τα γ και δ.
Τα α, δ λέγονται άκροι όροι, ενώ τα β, γ μέσοι όροι της αναλογίας.
Ο τέταρτος όρος δ της αναλογίας λέγεται και τέταρτη ανάλογος των α, β και γ.
Σε κάθε αναλογία ισχύουν οι ιδιότητες:
i) το γινόμενο των άκρων ισούται με το γινόμενο των μέσων όρων (τα χιαστί γινόμενα είναι ίσα).
ii) μπορούμε να εναλλάξουμε την θέση των μέσων όρων της. (Ισχύει και για τους άκρους)
Γραφική παράσταση σχέσης αναλογίας
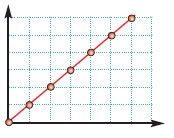
Τα σημεία που αντιστοιχούν στα ζεύγη τιμών (x, y) δύο ανάλογων ποσών
βρίσκονται πάνω σε μία ημιευθεία με αρχή την αρχή Ο (0,0) των ημιαξόνων.
Παράδειγμα
Δίνεται ο πίνακας:
Να γίνει η γραφική απεικόνιση των ζευγών (x, y) του πίνακα στο επίπεδο.
Ο πίνακας είναι πίνακας αναλογίας των ποσών x και y, με συντελεστή αναλογίας το α = 1
| x | 0 | 1 | 2 | 3 |
| y | 0 | 1 | 2 | 3 |