4.3 Área máxima ou mínima das figuras usando um barbante

Cálculo das área formadas usando um barbante
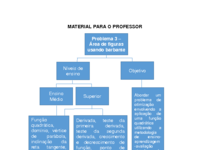
Público alvo: Ensino Médio ou Superior. Objetivo: Abordar um problema de otimização envolvendo a aplicação de uma função quadrática utilizando a metodologia de ensino-aprendizagem-avaliação através da resolução de problemas mediada pelo software GeoGebra.

Situação-problema 03
A professora de João propôs um trabalho para a turma dele no qual cada aluno deveria propor um problema usando os conhecimentos de funções. João pensou em explorar a construção de figuras geométricas que maximizam a área. Para a construção das figuras ele dispunha de um barbante de 10 decímetros de comprimento. Assim, ele pensou que com esse barbante ele poderia: a) construir um quadrado; b) construir uma circunferência; c) cortar em dois pedaços (não necessariamente de mesmo tamanho) de modo que um dos pedaços fosse usado para construir um quadrado e o outro para construir uma circunferência. Em qual situação João conseguirá a área máxima? E a área mínima? Resolva o problema proposto por João criticamente, apontando os conceitos envolvidos e as potencialidades/deficiências do problema.

Área de figuras usando um barbante

Como calculamos a área de um quadrado? E a área um círculo?
Se variarmos o tamanho do corte e as respectivas medidas para construir cada uma das figuras, a soma das áreas irá mudar ou será ser sempre a mesma, já que o tamanho do barbante utilizado é fixo? (Analise o aplicativo 'Área de figuras usando um barbante').
Como podemos escrever uma função que determina a área do quadrado em função do corte? E a área do círculo?
Qual o valor máximo da soma das áreas? E o mínimo? (Realize os cálculos e verifique no aplicativo)

Problema 3 - Área de figura usando barbante em PDF

Conversando com o professor