Elipse - Equação reduzida na forma canônica
ATIVIDADE 1
Movimente os pontos a e b no applet, e responda as questões abaixo.
a) Compare os valores de a e b com os denominadores da equação. O que você pode concluir?
b) Investigue no applet acima qual a relação existente entre a e b para que se tenha as seguintes posições da elipse:
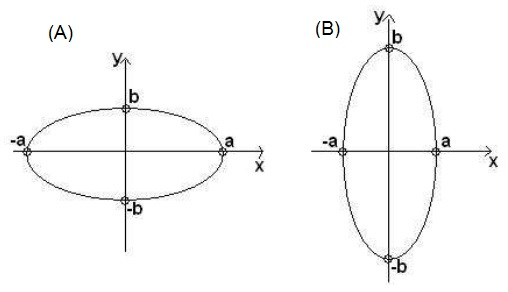
Continue investigando no applet...
c) O que acontece com a elipse se os valores de a e de b forem iguais?
d) O que o ponto azul representa?
e) Movimente o ponto azul sobre o eixo x e verifique o que altera na equação. O que você pode concluir?
f) Agora movimente sobre o eixo y e verifique o que altera na equação. O que você pode concluir?
g) O que altera na equação se o ponto azul estiver na posição (-4,2)?
g) Vamos ver se você entendeu. Quais serão as coordenadas do ponto azul se a equação da elipse for
? (Procure dar sua resposta e depois conferir no applet.)
Elipse - Dedução da equação reduzida na forma canônica
Para deduzir a equação utilizaremos a propriedade geométrica da elipse: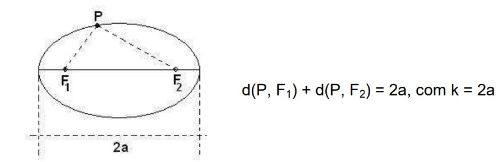
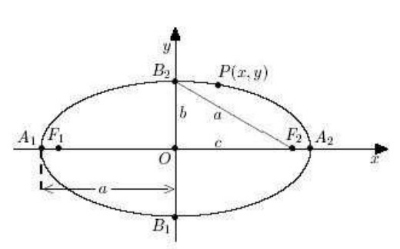


Fonte: Goulart (2009) (http://www.lume.ufrgs.br/handle/10183/18805)