Fracciones
1. Suma de fracciones
Distinguiremos dos casos a la hora de sumar dos fracciones:
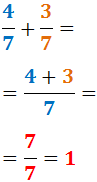
Caso 2: Fracciones con distinto denominador
Para poder sumar las fracciones tenemos que transformarlas en otras para que ambas tengan el mismo denominador.
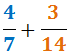El mcm de los denominadores es 14:
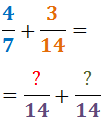
Calculamos los nuevos numeradores:
Para la primera fracción:
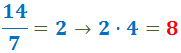Para la segunda fracción:
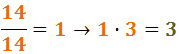Por tanto,
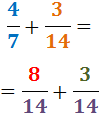
- Caso 1: Fracciones con el mismo denominador
- Caso 2: Fracciones con distinto denominador
- el numerador es la suma de los numeradores
- el denominador no cambia
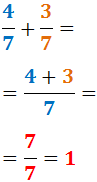
Caso 2: Fracciones con distinto denominador
Para poder sumar las fracciones tenemos que transformarlas en otras para que ambas tengan el mismo denominador.
- el nuevo denominador de ambas fracciones será el mínimo común múltiplo (mcm) de los dos denominadores
- el nuevo numerador (de cada fracción) será el resultado de: dividimos el denominador inicial por el nuevo denominador y después multiplicamos por el numerador inicial
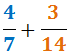El mcm de los denominadores es 14:
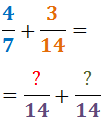
Calculamos los nuevos numeradores:
Para la primera fracción:
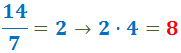Para la segunda fracción:
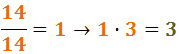Por tanto,
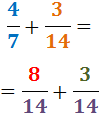
2. Producto de fracciones
El producto de dos fracciones es la fracción que
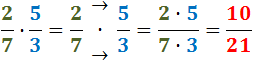
- su numerador es el producto de los dos numeradores
- su denominador es el producto de los dos denominadores
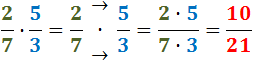
3. División de fracciones
La división de dos fracciones es la fracción que
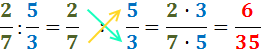
- su numerador es el producto del numerador de la primera fracción por el denominador de la segunda gracción
- su denominador es el producto del denominador de la primera fracción por el numerador de la segunda
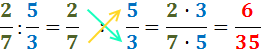
3. Fracciones Mixtas
Las fracciones mixtas o números mixtos están compuestas por un número entero (parte entera) y una fracción propia (parte decimal). Recordamos que una fracción es propia cuando su denominador es mayor que su numerador.
Por ejemplo:
El número que representa es la suma del entero y la fracción.
En el ejemplo, el número mixto es dos y medio:
El número que representa es la suma del entero y la fracción.
En el ejemplo, el número mixto es dos y medio:
4. Ejemplos, ejercicios y referencias
- Introducción: Concepto de fracción, ejemplos, tipos de fracciones y lectura de fracciones. Con Test sobre el tema.
- Simplificar Fracciones: cómo simplificar fracciones (máximo común divisor) y ejercicios resueltos
- Suma y Resta de Fracciones con el mismo denominador y con denominador distinto (mínimo común múltiplo).
- Producto y Cociente de Fracciones: multiplicar y dividir fracciones, ejemplos y ejercicios.
- Fracciones Equivalentes: fracciones distintas pero iguales. Ejemplos y ejercicios resueltos
- Fracción Generatriz de números decimales exactos, periódicos puros y periódicos mixtos.
- Fracciones Mixtas o números mixtos: concepto, test y ejercicios resueltos.
- Foro de Ayuda en Matemáticas