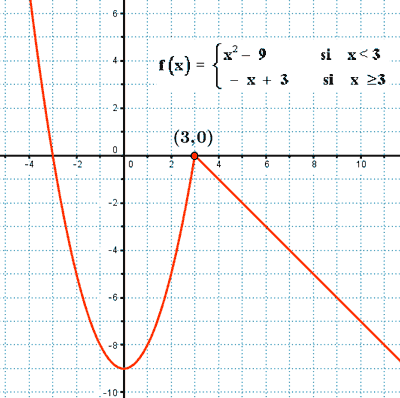FUNCIONES A TROZOS
EJERCICIO 1:
EJERCICIO 2:
EJERCICIO 3:
Representa y describe las características de las siguientes funciones:
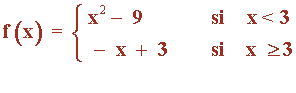1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = R
3) Puntos de corte:
Puntos de corte del eje Y:
x = 0 ⇒ f(0) = 0 - 9 = - 9 ⇒ (0 , -9)
Puntos de corte con el eje X:
• Para x < 3 : y = 0 , y = x2 - 9 ⇒ 0 = x2 - 9 ⇒
⇒ x = ±√9 = ± 3 , sólo x = - 3 < 3 ⇒ (-3 , 0)
• Para x ≥ 3 : y = 0 , y = - x + 3 ⇒ x = 3 ≥ 3 ⇒ (3 , 0)
Para dibujar la gráfica, además de los puntos de corte con los ejes, vamos a necesitar el vértice de la parábola:
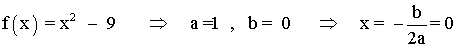Si x = 0 , hemos visto que y = - 9.
El vértice de la parábola es: (0 , - 9)
4) Continuidad:
(-∞ , 3) : la función es continua por ser una parábola, es decir, una función polinómica de segundo grado.
(3 , ∞) : la función es continua por ser una función lineal.
Veamos si f es continua en el punto x = 3 :
• f(x) = x2 - 9 : f(3) = 32 - 9 = 0
• f(x) = - x + 3 : f(3) = - 3 + 3 = 0
Como sí coinciden, f es continua en x = 3.
Por tanto, f es continua en todo R .
5) Monotonía:
• Si x < 3 f(x) = x2 - 9 : es una parábola con coeficiente a = 1 positivo, por tanto, es decreciente hasta su vértice (situado en x = 0), y creciente en el resto de valores menores que 3.
• Si x ≥ 1 f(x) = x - 2 : es una función lineal con pendiente negativa (m = -1), por tanto es decreciente.
Por tanto, f es creciente en: (0 , 3)
Y es decreciente en: (-∞ , 0) ∪ (3 , ∞)
Es claro, que existe un mínimo relativo en el vértice de la parábola (0 , 3) .
6) Asíntotas:
Ambas ramas de la función son polinómicas, por tanto, no tiene ninguna asíntota.
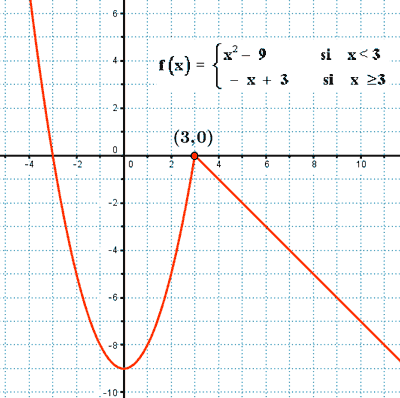
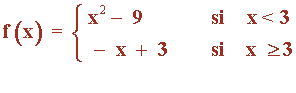1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = R
3) Puntos de corte:
Puntos de corte del eje Y:
x = 0 ⇒ f(0) = 0 - 9 = - 9 ⇒ (0 , -9)
Puntos de corte con el eje X:
• Para x < 3 : y = 0 , y = x2 - 9 ⇒ 0 = x2 - 9 ⇒
⇒ x = ±√9 = ± 3 , sólo x = - 3 < 3 ⇒ (-3 , 0)
• Para x ≥ 3 : y = 0 , y = - x + 3 ⇒ x = 3 ≥ 3 ⇒ (3 , 0)
Para dibujar la gráfica, además de los puntos de corte con los ejes, vamos a necesitar el vértice de la parábola:
Si x = 0 , hemos visto que y = - 9.
El vértice de la parábola es: (0 , - 9)
4) Continuidad:
(-∞ , 3) : la función es continua por ser una parábola, es decir, una función polinómica de segundo grado.
(3 , ∞) : la función es continua por ser una función lineal.
Veamos si f es continua en el punto x = 3 :
• f(x) = x2 - 9 : f(3) = 32 - 9 = 0
• f(x) = - x + 3 : f(3) = - 3 + 3 = 0
Como sí coinciden, f es continua en x = 3.
Por tanto, f es continua en todo R .
5) Monotonía:
• Si x < 3 f(x) = x2 - 9 : es una parábola con coeficiente a = 1 positivo, por tanto, es decreciente hasta su vértice (situado en x = 0), y creciente en el resto de valores menores que 3.
• Si x ≥ 1 f(x) = x - 2 : es una función lineal con pendiente negativa (m = -1), por tanto es decreciente.
Por tanto, f es creciente en: (0 , 3)
Y es decreciente en: (-∞ , 0) ∪ (3 , ∞)
Es claro, que existe un mínimo relativo en el vértice de la parábola (0 , 3) .
6) Asíntotas:
Ambas ramas de la función son polinómicas, por tanto, no tiene ninguna asíntota.