Integration by Parts
Integration by PartsIntegration by Parts is a special method of integration that is often useful when two functions are multiplied together but is also helpful in other ways.
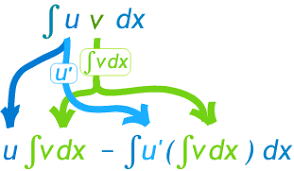
∫u v dx = u∫v dx −∫u' (∫v dx) dx
- u is the function u(x)
- v is the function v(x)
- u' is the derivative of the function u(x)
- Choose u and v
- Differentiate u: u'
- Integrate v: ∫v dx
- Put u, u' and ∫v dx into: u∫v dx −∫u' (∫v dx) dx
- Simplify and solve