Líneas de flujo
| Un concepto importante relacionado con los campos vectoriales (no necesariamente provenientes de un gradiente) es el de línea de flujo , definida de modo siguiente: Si F es un campo vectorial, una línea de flujo para F es una trayectoria c(t) tal que: r´(t) = F(r(t)) Es decir, F da el campo de velocidades de la trayectoria r(t). Osea que una linee de flujo es una trayectoria que obedece una dirección en un campo vectorial. |
Una línea de flujo consiste en dar una trayectoria r(t) tal que en cada punto de dicha trayectoria, la velocidad de la partícula corresponde en la dirección del campo vectorial.
Este tipo de problemas involucran integrales
Ejemplo de línea de flujo
consideremos un campo vectorial y y además consideremos una línea de flujo que inicie en (1,1)
visualización del campo
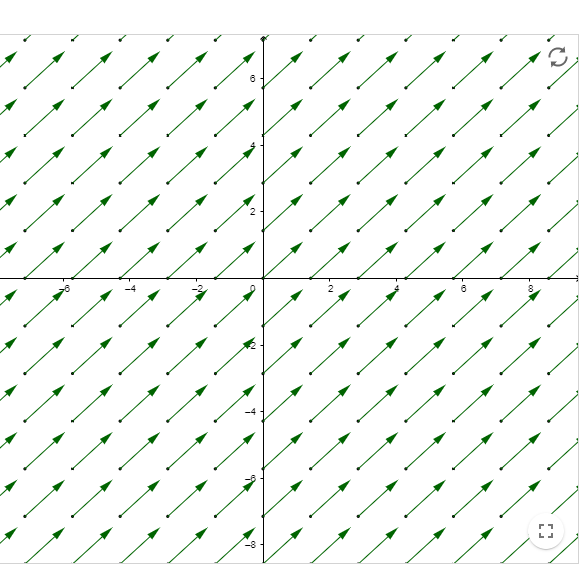
La función que buscamos tal que
entonces = (1,2)
Así ¿Cómo lo supimos? haciendo y también pero como hablamos de integrales indefinidas hace falta algo muy importante que es el + C entonces tenemos y encontrando esas constantes tales que nos de como resultado (1,1) obtenemos pues al hacer nos queda