Sistema cartesiano
No vídeo a seguir, o professor Ferretto explica noções básicas do Plano Cartesiano. Assista até o minuto 7:34.
Sistema Cartesiano.
Considerando dois eixos x e y que são perpendiculares em um ponto O, diz-se que o plano definido por esses eixos é todo o ² e chamamos esse plano de Plano Cartesiano. Esse ponto O é chamado de origem do plano cartesiano. Chamamos o eixo x de eixo das abscissas e o eixo y de eixo das ordenadas.
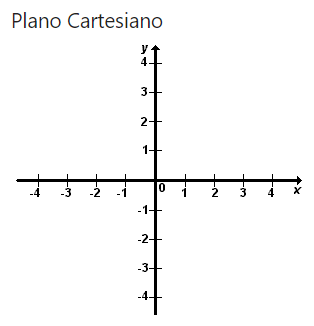
Os eixos cartesianos x e y dividem o plano em quatro regiões chamadas quadrantes.
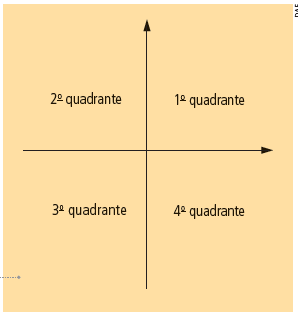
Construindo um plano cartesiano.
Para construir um plano cartesiano, traçamos duas retas numéricas perpendiculares que se intersectam no ponto que representa o zero de cada uma delas. Elas serão chamadas de eixos.
Repare que as setas indicam o sentido crescente dos números que seus pontos representam.
Lembrando que:
Eixo horizontal: é o eixo das abscissas, ou eixo x.
Eixo vertical: é o eixo das ordenadas, ou eixo y.
Para construir um plano cartesiano usando o GeoGebra, você deve seguir os passos:
1) Crie dois pontos A e B com a ferramenta ponto de forma que A e B estejam em uma reta horizontal;
2) Clique na ferramenta Reta e selecione os pontos A e B;
3) Clique na ferramenta Reta Perpendicular, selecione a reta e o ponto A;
4) Clique na ferramenta ângulo, após, clique nas duas retas criadas, f e g;
5) Após, verifique que o ângulo entre as duas retas é 90 graus;
6) Sendo a reta que contém A e B o eixo x, e a reta que contém A e é perpendicular a reta que contém A e B sendo o eixo y, temos então o plano cartesiano.
Construa aqui o plano cartesiano.
Utilize o campo abaixo para relatar caso você tenha alguma dúvida.
Localizando pontos no sistema cartesiano:
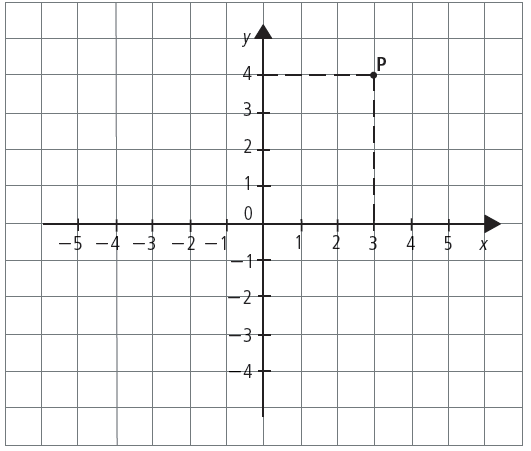
Localizamos o ponto P (conforme a imagem anterior) no plano:
• 3 no eixo x;
• 4 no eixo y.
A localização de P é dada pelo par ordenado (3, 4) onde 3 e 4 são as coordenadas do ponto P: 3 é a abscissa e 4 é a ordenada.
Estabeleceu-se que o primeiro elemento do par sempre será a abscissa e o segundo elemento, a ordenada do ponto.
Portanto, (3, 4) é o par ordenado que representa o ponto P no plano.
Escrevemos P(3, 4).
Mova o ponto P pela tela e observe suas coordenadas.
Na atividade a seguir você precisa ajudar o Ash a capturar o pokémon!
Siga as instruções:
1. Clique no botão "Iniciar";
2. Em "Alvo" digite as coordenadas do Pokémon;
3. Clique no botão "Lançar";
obs: O pokemón é grande, mas o ponto exato que você precisa lançar a pokebola está destacado em vermelho.
Capture o Pokémon!
Vamos encontrar o submarino!
Exercícios:
Leia atentamente cada questão e responda o que se pede.
Questão 1: Escreva nos campo "resposta" os pares ordenados que representam os pontos A, B, C, D, E, F e G.
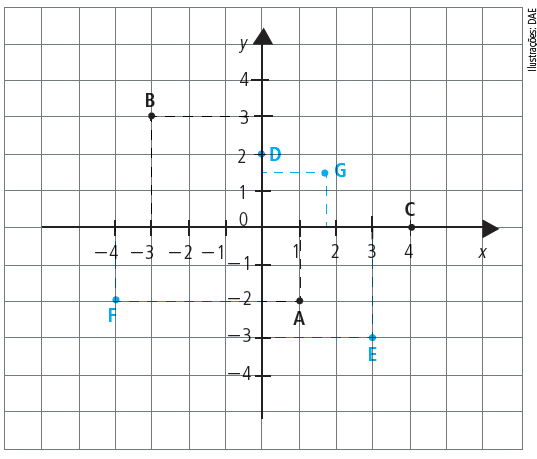
Resposta:
Questão 2: (Saresp) Observe a figura abaixo. Em qual posição está a roda da frente do carro?
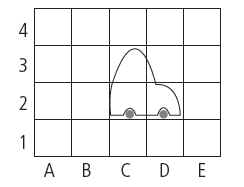
Resposta:
Questão 3: Observe a planta de uma sala de aula. Nela, há carteiras individuais dispostas em linhas e colunas.
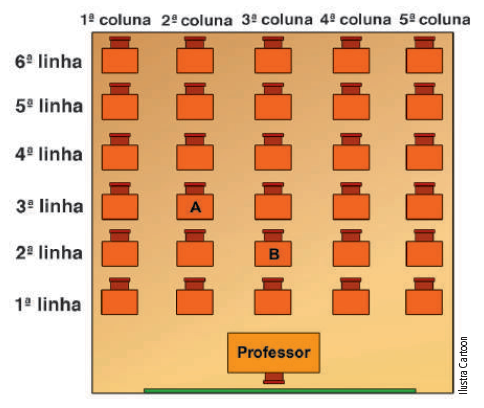
Responda:
a) Qual é a posição (coluna; linha) da carteira A? b) Qual é a posição (coluna; linha) da carteira B?
Questão 4: Dê as coordenadas de cada ponto do plano cartesiano.
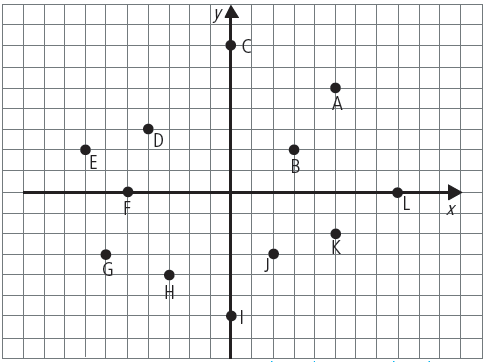
Resposta:
Questão 5:
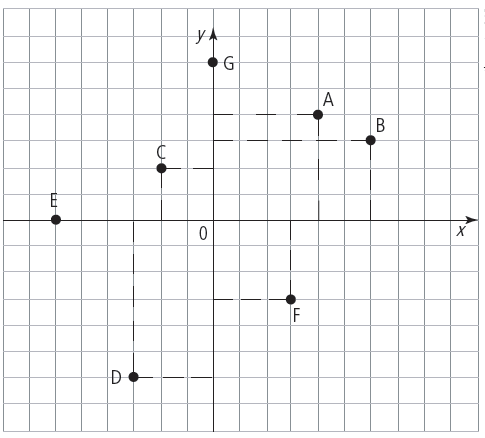
Indique qual dos pontos A, B, C, D, E, F e G, abaixo, verifica cada uma das seguintes afirmações:
a) A abscissa é igual à ordenada. b) A ordenada é negativa. c) A abscissa é metade da ordenada. d) A abscissa é o dobro da ordenada. e) A ordenada é nula. f) A abscissa é nula.