Função do 2º grau - Parâmetros e Discriminante
Estamos estudando o comportamento do gráfico da função quadrática descrita algebricamente por f(x)=ax²+bx+c, onde a, b e c são números reais, a não nulo, e x um valor real qualquer.
Iremos explorar visualmente a relação entre os parâmetros a, b e c em f(x)=ax²+bx+c e o gráfico no plano cartesiano, mais especificamente sobre o comportamento do gráfico quando alterados seus
parâmetros.
Na tela abaixo, explore livremente os parâmetros a, b e c, altere seus valores, faça aparecer a função quadrática.
Modifique os valores dos coeficientes a e c, e perceba as alterações que ocorrem no gráfico.
Alterne entre valores negativos e positivos o parâmetro a. Que diferença você identifica visualmente entre o gráfico cujos valores de a são negativos e aqueles cujos valores de a são positivos?
1. Quando a > 0, a concavidade da parábola é voltada para _____
2. Quando a < 0, a concavidade da parábola é voltada para _____
Vamos estudar o coeficiente c. Tome os valores de c indicados: c=-4, c=-2, c=0, c=3, c=5 e encontre o valor de Y em que ocorre a intersecção do gráfico da função quadrática com o eixo Y em cada caso de c.
3. Qual a influência do coeficiente c?
E o coeficiente b?
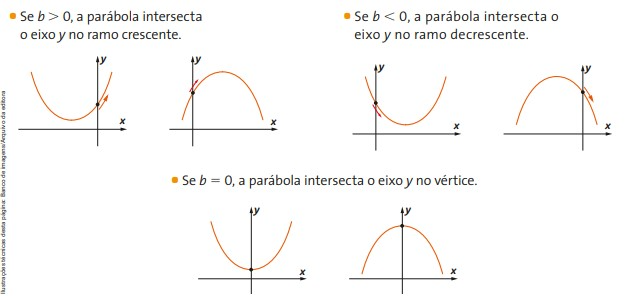
O parâmetro b indica se a parábola intersecta o eixo y no ramo crescente ou decrescente da parábola.
Discriminante
Discriminante é a parte da fórmula de Bháskara que está sob a raiz quadrada.
O cálculo do discriminante é feito substituindo os valores dos coeficientes da equação na
seguinte fórmula: = b²-4.a.c
Se 0, é possível determinar as raízes da equação do 2º grau. Através da fórmula de Bháskara.
x =
Agora, vamos utilizar o para descobrir quantas raízes reais a função possui. Para isso, mexa no parâmetros a, b e c para mudar o valor do determinante e responda as questões.
4. Se o >0 tem-se:
5. Se o =0 tem-se:
6. Se o <0 tem-se:
Imagem para o exercício
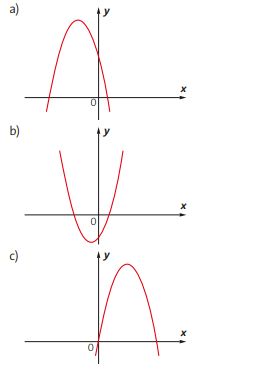
7. Imagem a.
8. Imagem b.
9. Imagem c.
10. Determine, caso existam, os zeros de cada função.
a) f(x) = x² -7x+10 b) f(x) = x²-6x+9 c) f(x) = -x²+x-7 d) f(x) = -4x²+4
e) f(x) = +6x f) f(x) = -2x²+3x-5 g) f(x) = 3x²+x-2 h) f(x) = -x²+8x-16
a)
b)
c)
d)
e)
f)
g)
h)