Meat-Slicer Method
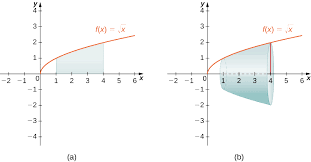
To find the volume of this solid of revolution, use the meat-slicer method:
1. Find an expression that represents the area of a random cross-section of the solid (in terms of x). This cross-section is a circle with a radius of 2 sin x:
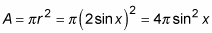2. Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid. This time, the limits of integration are from 0 to π/2:
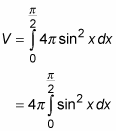3. Evaluate this integral by using the half-angle formula for sines:
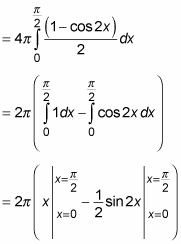
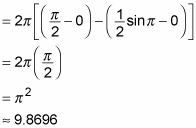So the volume of this solid of revolution is approximately 9.8696 cubic units
2. Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid. This time, the limits of integration are from 0 to π/2:
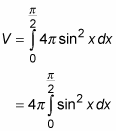3. Evaluate this integral by using the half-angle formula for sines:
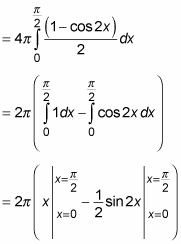
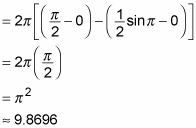So the volume of this solid of revolution is approximately 9.8696 cubic units