M2 Lesson 12: Angles Associated with Parallel Lines
Use the following pictures as notes to answer questions on the tasks.
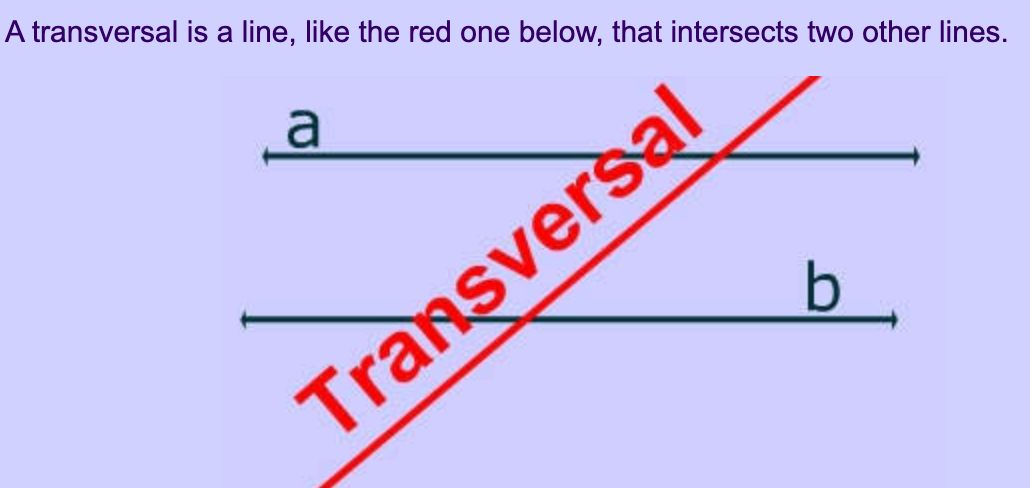
What did you notice about the measures of corresponding angles? What type of transformation would support your reasoning (translation, reflection, or rotation)?
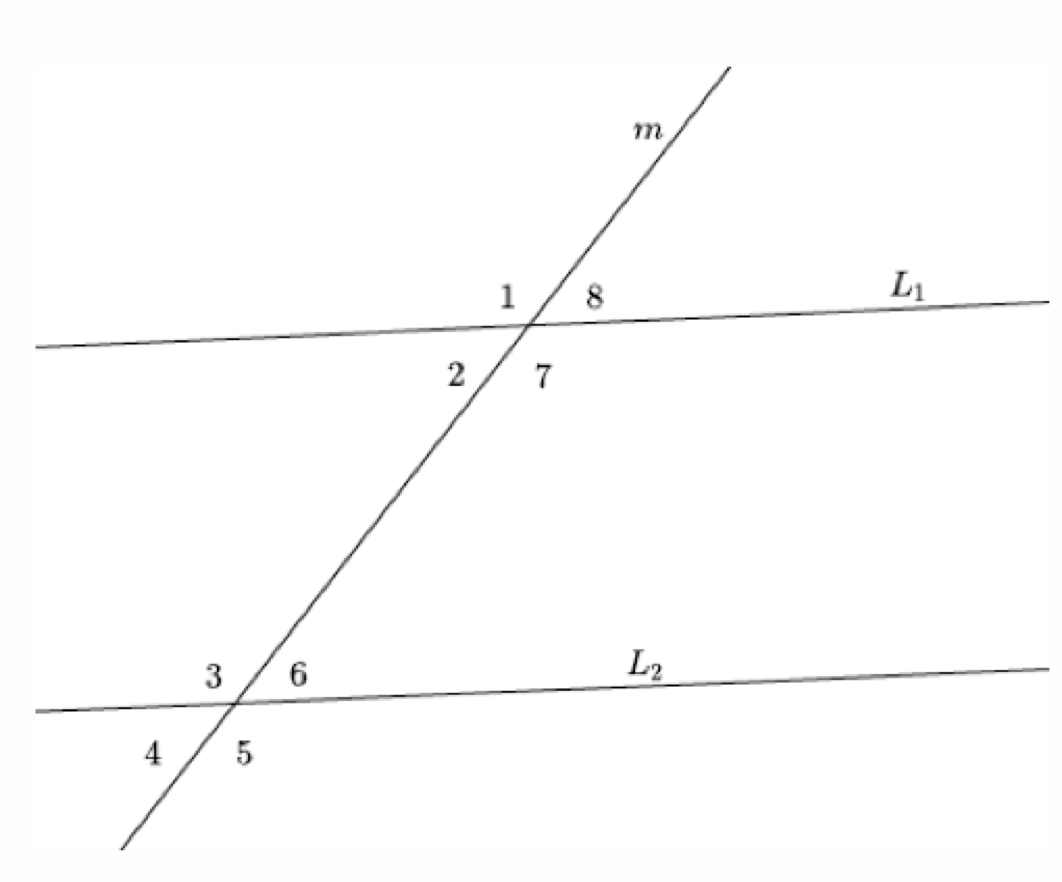
Angles that are on the same side of the transversal in corresponding positions (above each of Line 1 and Line 2 or below each of Line 1 and Line 2) are called corresponding angles. Name a pair of corresponding angles in the diagram above.
When angles are on opposite sides of the transversal and outside the lines Line 1 and Line 2, they are called alternate interior angles. Name a pair of alternate interior angles.
When angles are on opposite sides of the transversal and outside the lines Line 1 and Line 2, they are called alternate exterior angles. Name a pair of alternate exterior angles.