Ruffini's Rule
What is it?
Ruffini's Rule is a shortcut method for dividing a polynomial by a linear factor of the form (x-a).
- This method reduces the polynomial and the linear factor into a set of numeric values.
- After these values are processed, the resulting set of numeric outputs is used to construct the polynomial quotient and the polynomial remainder.
Step 1: Make sure the terms in the polynomial are in descending order. If a term is missing, add it in with a coefficient of zero.
This is going to be your dividend.
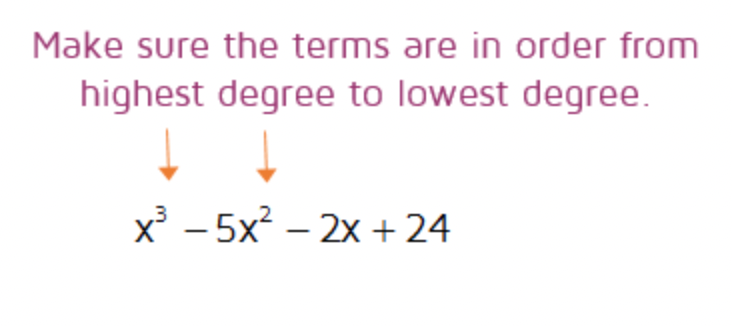
Step 2: Set the linear factor equal to zero. Solve for x.
This is going to be your divisor.
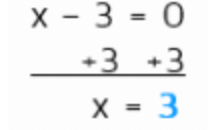
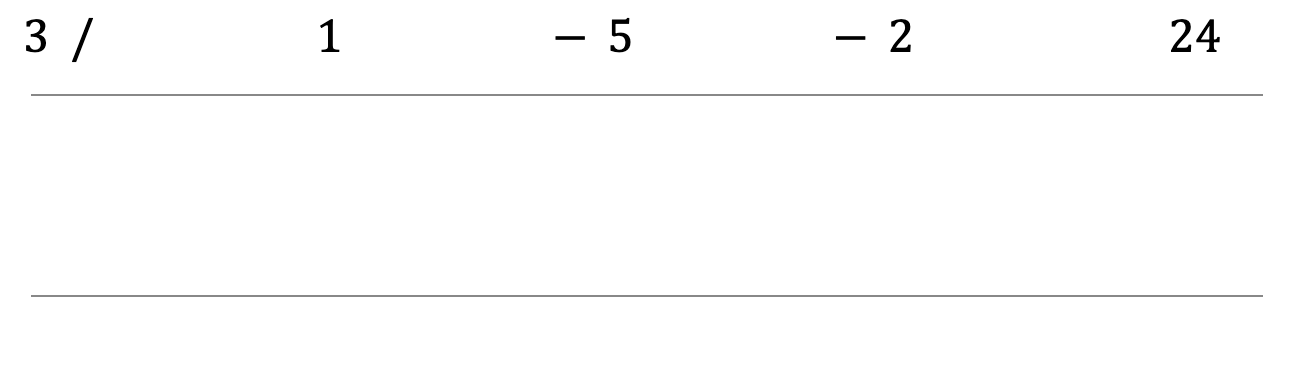
Step 3: Set up the problem. Make sure to put the divisor and the dividend in the correct locations.
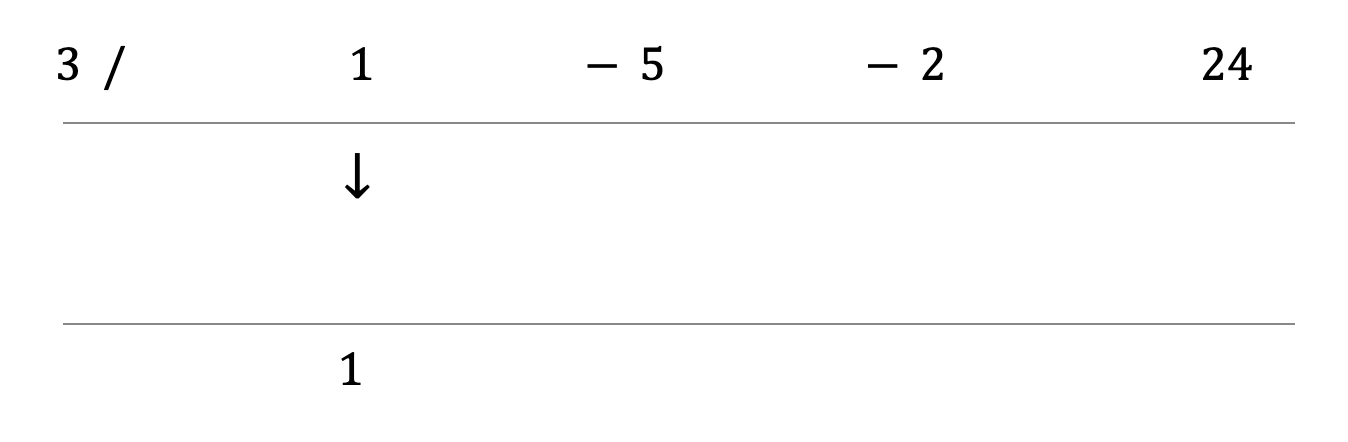
Step 4: Bring down the first coefficient. When you're dividing by x-a, the coefficient will always be the same.
Step 5: Multiply the divisor by the number you brought down. Put the product in the next column.
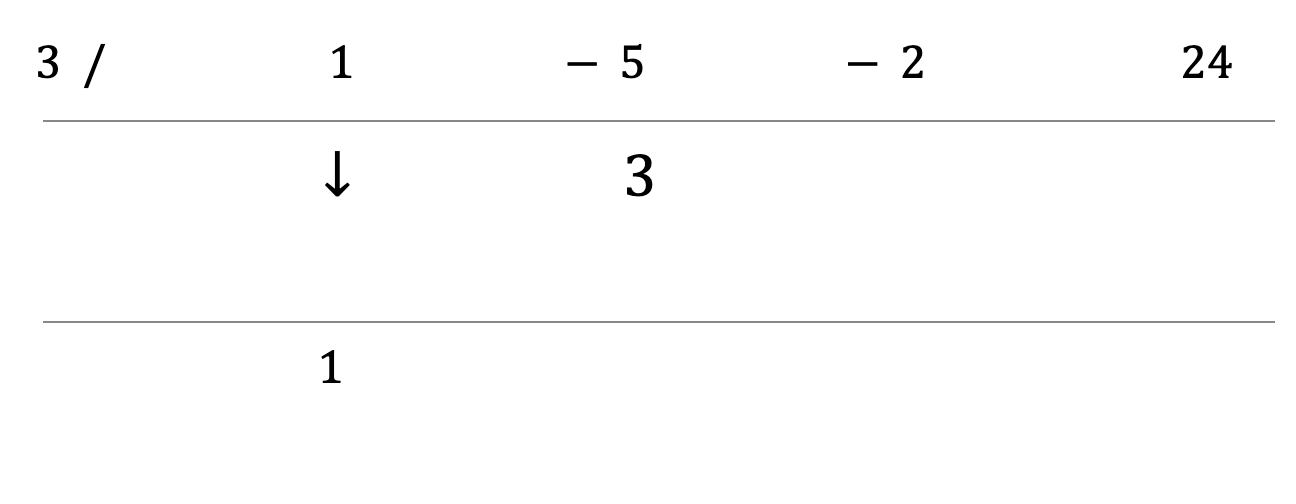
Step 6: Add the numbers in the second column.
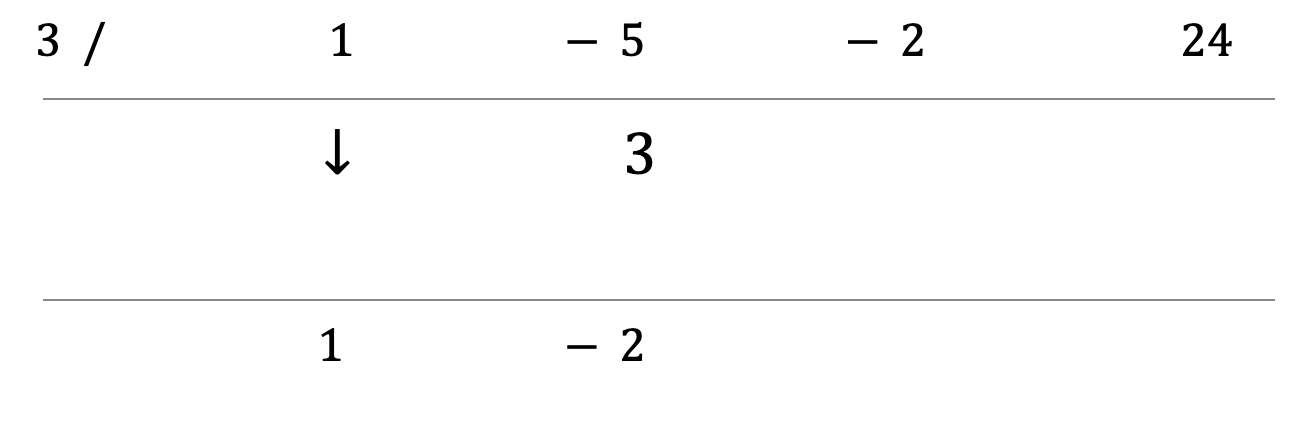
Step 7: Repeat steps 5 and 6 for the remaining coefficients.
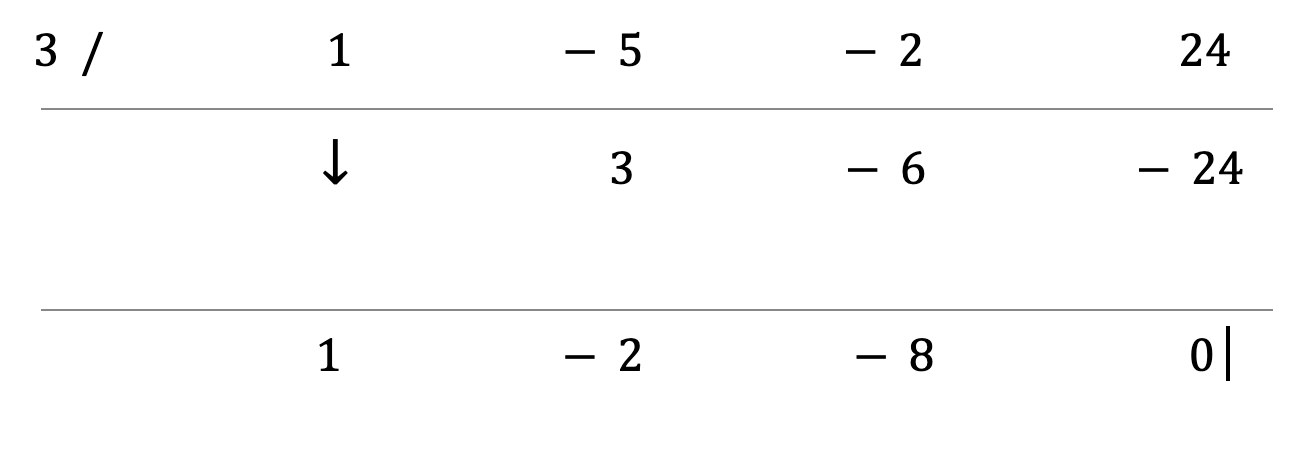
Step 8: Write the answer.
The numbers you wrote down on the bottom row of the coefficients of the answers.
The last number on the right is the remainder.
The degree of your answer will always be one less than what you started with.
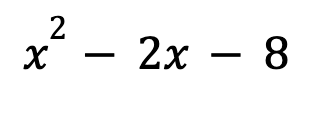
How do you feel about this so far?