Definition
Anhand des Einführungsbeispiels haben wir gesehen, wie wir die Ober- bzw. Untersumme berechnen können.
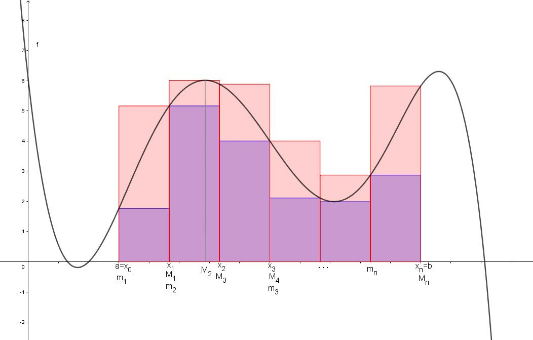
Zuerst muss ein Intervall in kleinere Teilintervalle zerlegt werden.
Dazu müssen wir eine Zerlegung definieren:
Definition: Zerlegung
Eine Zerlegung eines Intervalls ist eine endliche Folge von Unterteilungspunkten.
Also .
Für die Unterteilungspunkte gilt:

Die Längen der der Teilintervalle , , ... werden mit , , ... bezeichnet.
Nun können wir die Obersumme und Untersumme definieren:
Definition: Ober- und Untersumme
Es sei eine im Intervall stetige Funktion und eine Zerlegung von .
Weiters seien die Minimumstellen von und die Maximumstellen von in den jeweiligen Teilintervallen.
Dann ist die Untersumme von im Intervall mit der Zerlegung :
Die Obersumme von im Intervall mit der Zerlegung ist:
Schreibe die beiden Definitionen in dein Heft!