第二节 常见的离散型随机变量的分布
一、等概率分布
顾名思义，等概率分布是指每一个可能出现情况的概率取值都是相等的。比如抛硬币、抛骰子等，一般将等概率分布称为“古典概型”。 以抛硬币为例，将反面记为0分，正面记为1分，随机变量为抛硬币一次的分数，那么的分布可以写为： 设随机变量有个取值a1,a2,...,an，每个取值出现的概率相等，那么，随机变量的概率密度函数为： 二、伯努利分布
伯努利分布，也叫0-1分布或两点分布。凡是随机试验只有两个可能的结果，常用伯努利分布描述，如产品是否格、人口性别统计、系统是否正常、电力消耗是否超负荷等等。其概率分布的列表式为：
其概率密度函数为：
| | 1 | 0 |
| | |
三、二项分布
二项分布，也叫重伯努利分布，是指反复多次重复伯努利实验，比如重复抛骰子计算某个点出现几次的概率问题，射击的命中次数和命中率问题，一批种子的发芽率问题，药物治疗病人是否有效的问题，产品的不合格率问题等都要用到二项分布。实际上，在现实生活中一个事件的发生能归并为两种结果，并且事件每次发生都是独立的，我们都可以尝试用二项分布来解决一些问题。
一般设伯努利实验有两种可能的结果A和B，事件A发生的概率是，事件B发生的概率是，独立地重复进行次该实验，设随机变量表示事件A发生的次数，我们称随机变量服从参数为的二项分布，记为，其概率密度函数为：
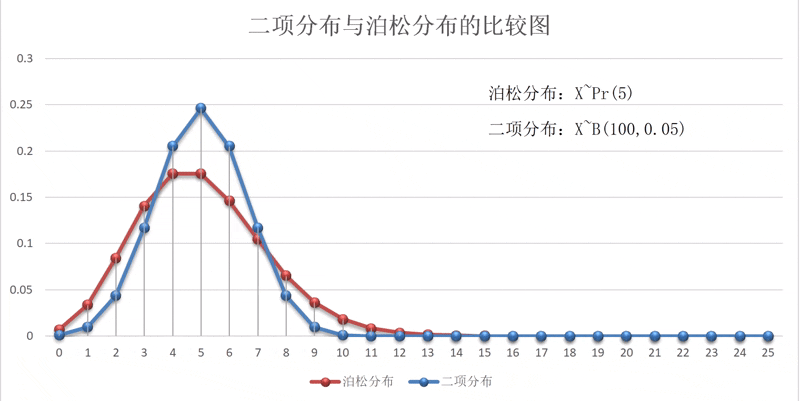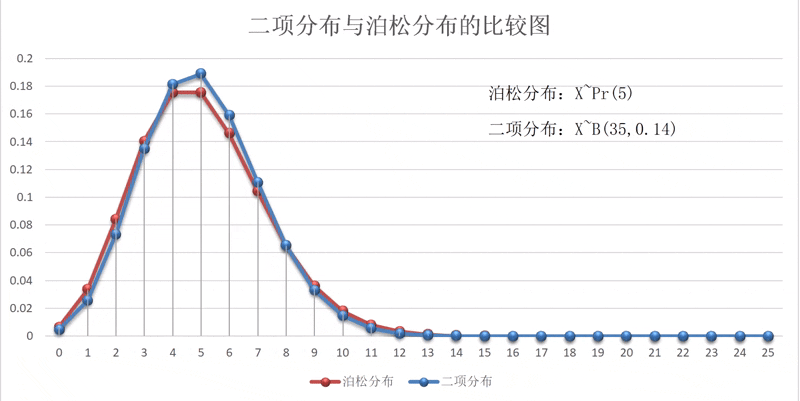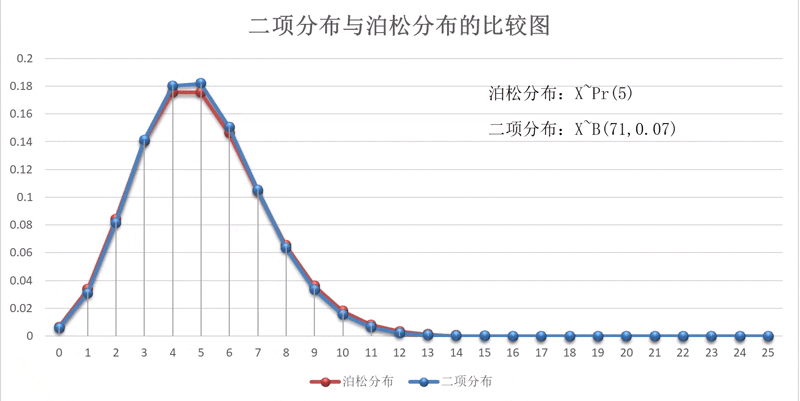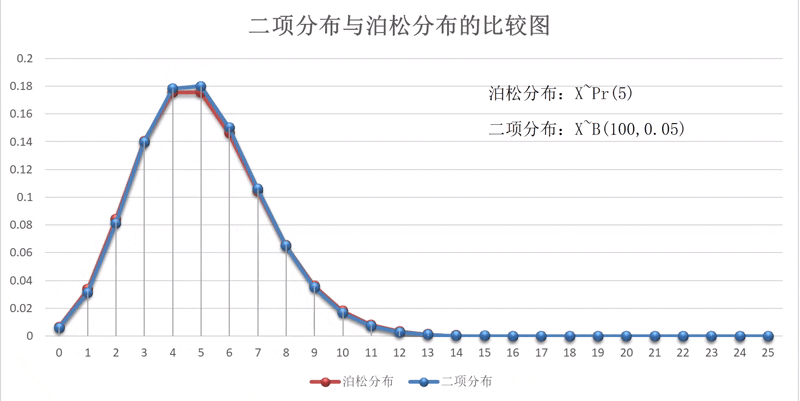
以下四张图为,时的二项分布概率图，从图中可以看出，一次事件发生时的概率不同，其概率分布的图形走向也不同，但总有发生次数最大的概率呈现。比如，在分布中，某一事件发生5次的概率最大，而在分布中，概率值最大的发生次数是3次。见图2-1。
图2-1 四个二项分布图
在现实生活中，有时人们更关心最有可能的发生次数是多少。比如，在射击实验中最有可能击中的次数是多少，在产品检验中最有可能检出不合格数是多少等。要解决此类问题，可以应用二项分布的性质1进行计算。
性质1： 设，则最可能的值是。如是整数，则也是最可能的值，这里为取整函数，例如。
证明 考虑如下概率比，并令其大于1，这保证随增大而严格增大，
,即（,从而,即
时,故当时，严格增加。同上， 时
，即当时，严格下降，由此可证得性质1。
设重伯努利取得概率最大值的为，如果想要知道在中排名地位如何，则只需要计算。
，则当时，。
二项分布给我们的启示为：①小概率事件有存在的空间，只要足够大，就有发生的可能；②最有可能的发生次数，由可大体估算；③固定，随着的增大，其取值的分布趋于对称。
四、几何分布
几何分布也是以伯努利分布为基础的一种特殊分布，它主要解决在次重复独立实验中，某个我们关心的结果在某次（值）时第一次出现的概率。主要应用场景如在已知某器件报损概率的情况下，测算其正常使用寿命。或在中奖概率一定的情况下，需要多长时间能中的大奖。
设随机试验有且只有两种结果A和B，A出现的概率是,B出现的概率是1-，反复进行该随机试验，随机试验之间彼此独立，随机变量X表示A第一次出现时随机试验进行的次数，此时我们称随机变量X服从几何分布，记为，其概率密度函数为：
之所以该分布被称为“几何分布”，由其概率密度函数不难得出，其分布列各项构成等比数列，而等比数列，又称几何数列，这源于除了首项和末项之外，每一项都是前后两项的几何平均数。
以下三幅图（见图2-2）是几何分布在不同值和值时的形态图。第一图为假设A事件发生概率，随机变量X在10次重复试验中，分别在第时第一次出现A的概率分布图。从图中可以看出，在第一次就出现A事件的概率最高，然后概率值逐渐降低。事实上，当我们尝试增加值时，就会得到近似的曲线，其概率会无限接近于0，如第二图（）。而如果改变事件成功概率，则会影响曲线的弯曲程度，如第三图（）。
图2-2 三个几何分布图
五、超几何分布
超几何分布也是非常常见的一种分布，对其模型建立一般是这样的：在个物品（如产品）中有指定商品（如废品）个，不放回地抽取个，随机变量表示抽中件指定商品，此时我们称随机变量服从超几何分布，记为，其概率密度函数为：
min为正整数且)
超几何分布其实在性质上与几何分布没有关系，之所以叫这个名字，是因为它的分布列的每一项正好是某个超几何级数中的项，是几何数列的扩展，故命名为“超几何”。
以下是 的超几何分布图（见图2-3），其中，否则在达到阈值时，部分值的概率无意义。
图2-3 超几何分布图
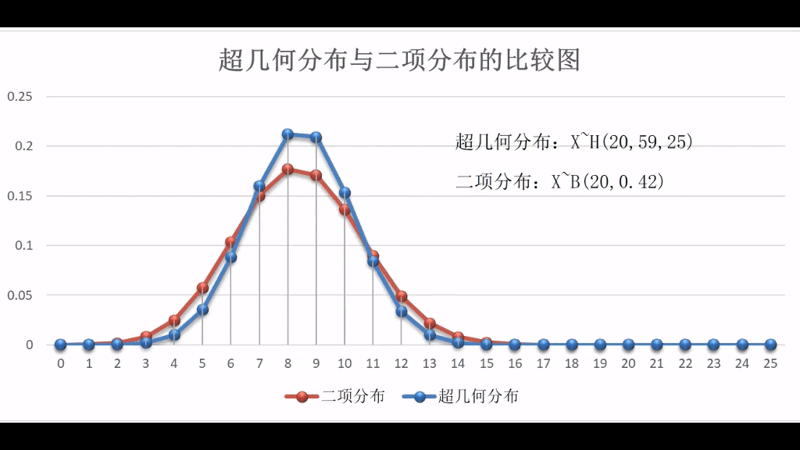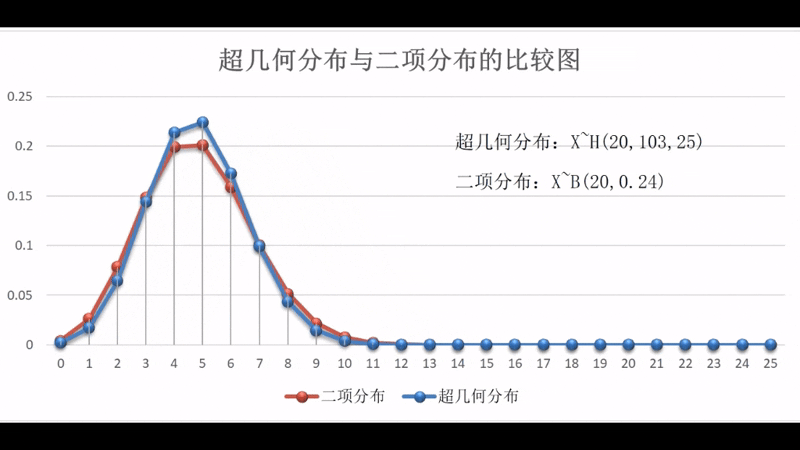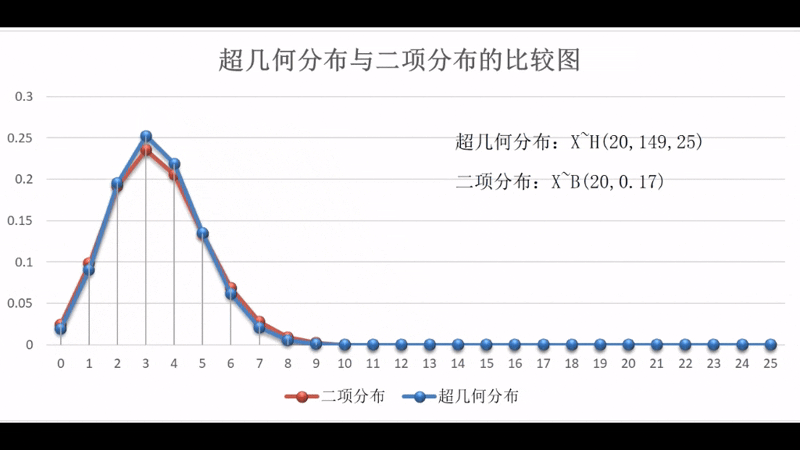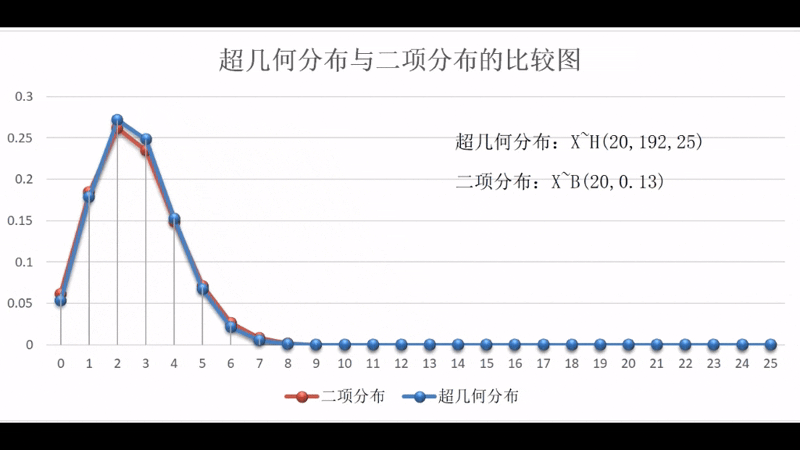
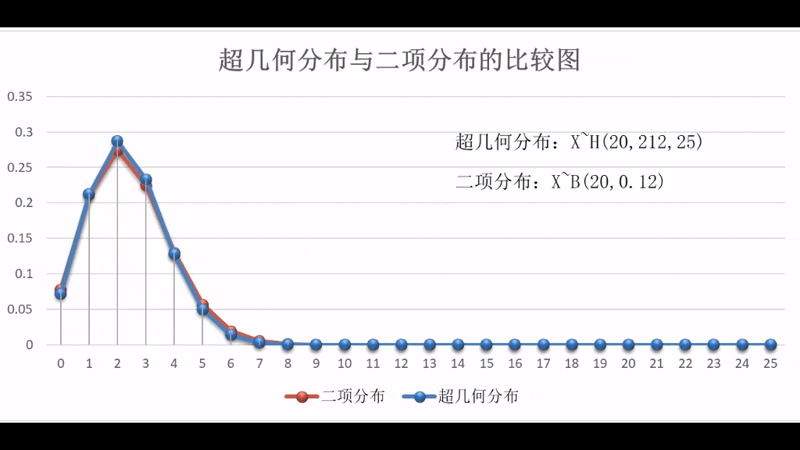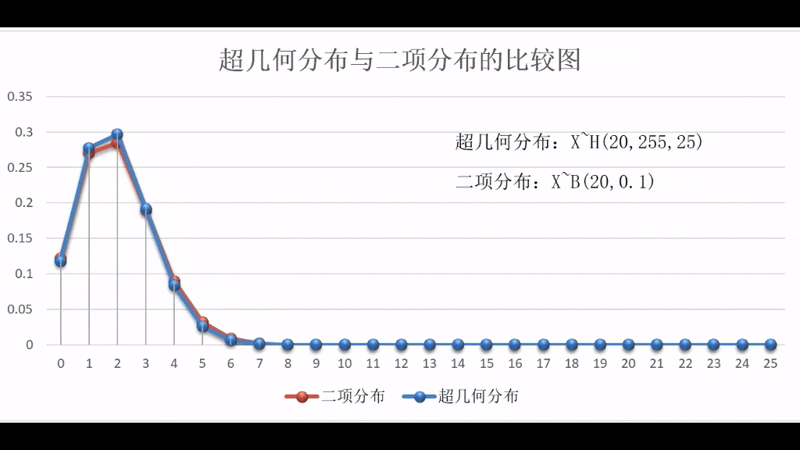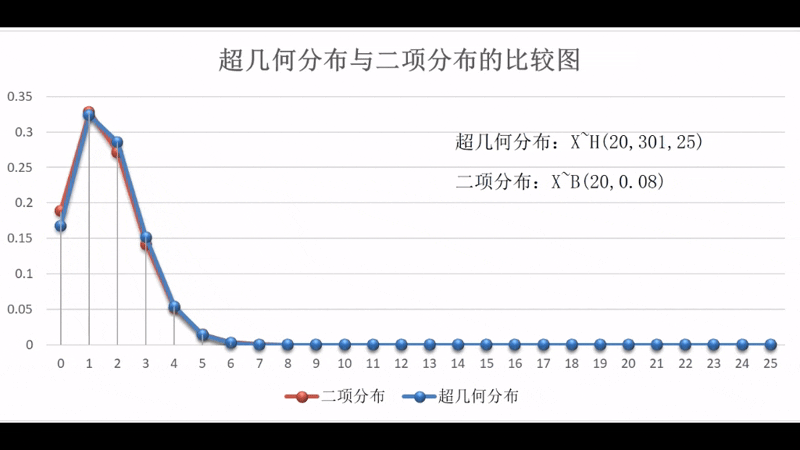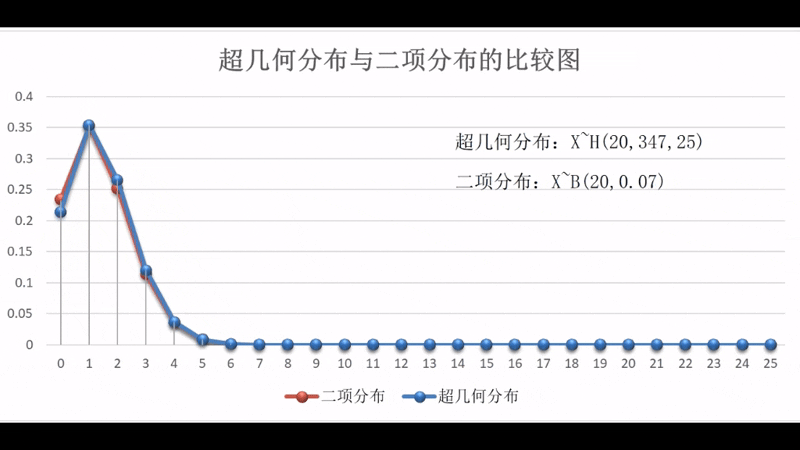
超几何分布从图形上来看与二项分布非常相似，实际上，这两个分布有内在的紧密联系，即样本个数越大超几何分布和二项分布的对应概率相差就越小，当样本个数为无穷大时，超几何分布和二项分布的对应概率就相等，换而言之，超几何分布的极限就是二项分布。
两者之间的动态关系可扫描右边的二维码观看演示。演示区中的超几何分布的参数为，二项分布的参数为，变化参数为，变化区间为。两个分布在和时的状态比较图为参见图2-4。
图2-4 超几何分布与二项分布比较图
超几何分布在实际生活中也有相当广泛的应用场景，比如生产企业的质量检测环节，总体个数的最大似然估计，统计假设检验问题等。
六、泊松分布
泊松分布适合于描述单位时间或空间内随机事件发生的次数。比如某一个服务设施在一定时间内到达了多少人，电话交换机接到了多少次呼叫，汽车站台的候客人数，机器出现的故障次数，显微镜下单位分区内的细菌分布数等。
泊松分布是指某个随机事件在一定的时间或空间独立发生，已知该事件发生的平均次数，且为有限值，记为，随机变量表示事件发生的次数，如果服从参数为的泊松分布，则记为，其概率密度函数为：
以下是的泊松分布图（见图2-5）。
图2-5 泊松分布图
泊松分布的参数是单位时间（或单位空间）内随机事件的平均发生率。比如，根据统计，2015年共发生17次航空灾难，而这一年共有3400万个航班，即这一年的全球航班失事概率为1/200万次。如果我们将这一概率视为近一段时间飞机失事的发生概率，即，而将1亿个航班（近三年）作为考察区段，即个，则。
图2-6 二项分布与泊松分布比较图
以上四种离散分布的动态演示图可以用数学软件Geogebra画出，参见https://www.geogebra.org/m/xfjsmv7v。学习者可以调整各分布的参数查看图形变化过程，也可下载研究。如在手机端操作，请扫描右边的二维码。其图形呈现如图2-7。
图2-7 四种分布在Geogebra中的呈现