4. Ángulo entre dos planos/Ángulo entre una recta y un plano
Ángulo entre dos planos
El ángulo formado por dos planos es igual al ángulo determinado por los vectores normales de dichos planos y entre planos y rectas lo podemos establecer con un vector paralelo a la recta (el vector dirección, por ejemplo) y un vector normal.
Para ello conviene recordar que dado un plano π de ecuación π: Ax+By+Cz+D=0, un vector perpendicular a dicho plano (vector normal al plano) es n=(A,B,C)
Así, si tenemos:
- π1 plano con vector normal n1.
- π2 plano con vector normal n2.
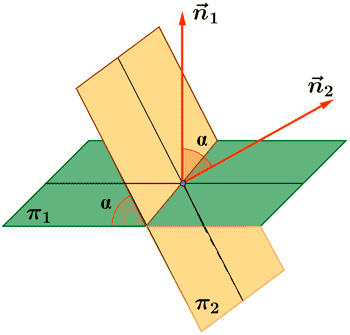
Entonces:
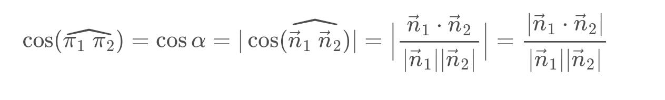
Por lo que para obtener nos queda lo siguiente:
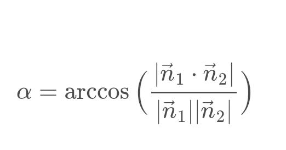
De acuerdo a lo anteriormente mencionado, tomamos los vectores normales
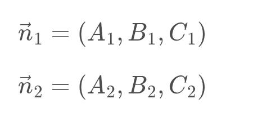
Y finalmente obtenemos la fórmula para calcular el ángulos entre planos
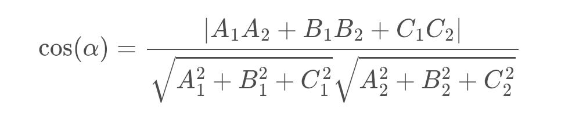
EJEMPLO:
Hallar el ángulo que forman los planos:
 Obtenemos sus vectores normales
Obtenemos sus vectores normales
 Aplicamos la fórmula
Aplicamos la fórmula
 Y obtenemos que
Y obtenemos que

 Obtenemos sus vectores normales
Obtenemos sus vectores normales
 Aplicamos la fórmula
Aplicamos la fórmula
 Y obtenemos que
Y obtenemos que

EJERCICIO: Dados los planos: π1:3x−y+2z+1=0 π2:2x+y−5z−1=0 Encontrar el ángulo que forman.
Ángulo entre una recta y un plano
Una recta puede estar incluida en un plano, ser paralela a él, o bien ser secantes. El ángulo entre ellos se define de la siguiente manera en cada caso:
- Si la recta está incluida en el plano o ambos son paralelos, la recta y el plano forman un ángulo de 0∘.
- Si la recta y el plano son secantes, definimos el ángulo α entre la recta y el plano como el ángulo que forma la recta con su proyección ortogonal sobre el plano.
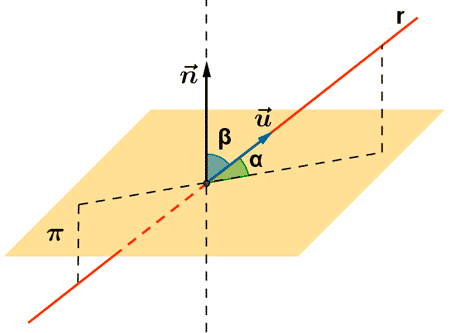
Si definimos el ángulo entre la recta y el plano como el ángulo entre la recta y su proyección ortogonal sobre el plano, podemos realizar el cálculo a partir del ángulo entre el vector director de la recta y el vector normal al plano.
Por tanto, si tenemos:
- π: plano.
- r: recta.
- s: recta perpendicular al plano.
- vr: vector director de la recta r.
- vp: vector director de la proyección de la recta sobre el plano.
- n: vector normal (perpendicular) al plano (y director de s).
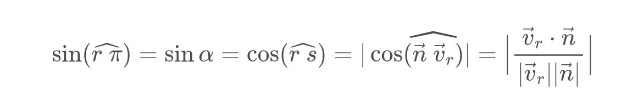
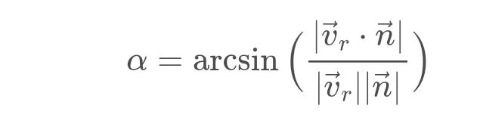
Además, si vr=(v1,v2,v3) y n=(A,B,C), podemos expresar la fórmula anterior en componentes como:
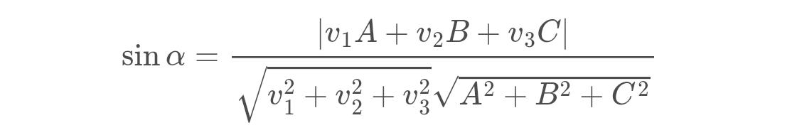
EJEMPLO:

EJERCICIO: Calcula el ángulo formado por la recta r y el plano π: r:(x,y,z)=(5,1,0)+k⋅(0,1,3) π:3x−y+2z+1=0