Elements per videojocs
Una de les aplicacions de les fractals és la generació d'elements per a videojocs. Mira els següents exemples:
a) Terrenys:
https://www.shadertoy.com/view/3dXcW2
b) Aigua:
https://www.shadertoy.com/view/Ms2SD1
c) Escenes:
https://www.shadertoy.com/view/DtBGzt (cada cop que fas clic a la imatge es regenera)
Quin exemple t'ha agradat més?
Select all that apply
- A
- B
- C
Anem a veure com es fa la generació de terrenys (tipus l'exemple que tens a la imatges següent)

Començarem recordant la Corba de Koch amb aquest vídeo:
Si hi penses, a la Corba de Koch, es fa exactament el mateix a cada iteració:
1r) Dividir cada segment en tres parts.
2n) Elevar la part del mig a l'alçada adient perquè quedi un triangle equilàter.
3r) Anar repetint els passos anteriors en els segments que han quedat.
Què creus que passaria no elevessis la part del mig la mateixa distància en cada cas? (descriu amb les teves paraules com podria ser la forma que quedaria)
Observa doncs què passa si cada cop dividim els segments pel mig i els elevem una quantitat aleatòria (diferent en cada cas, que fins i tot pot ser negativa, de manera que aleshores el que fem és "baixar"):
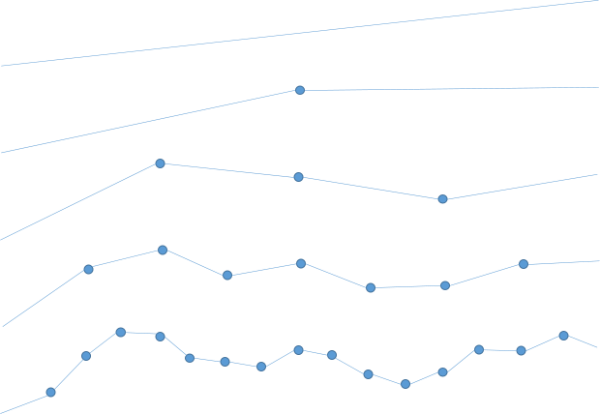
Si això ho fem en 2D, és a dir sobre un quadrat enlloc d'un segment, observa que al final ens queda una superfície que té punts més alts i altres més baixos:
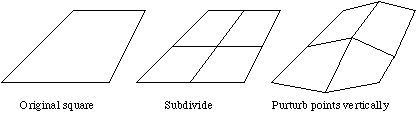
Si repetim aquest procés, fixa't quina aparença acaba tenint:
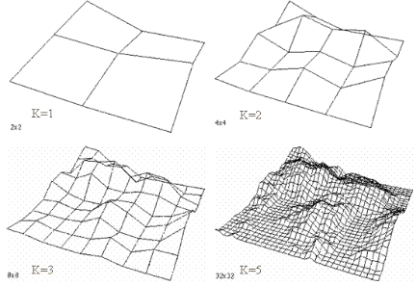
A què es podria assemblar la forma de la superfície que queda al final?
Ara ho faràs tu amb Geogebra. Primer prova aquest applet on ja està fet en 2D:
En aquest applet anterior d'exemple s'ha usat una entrada d'aquest estil:
P = ( x(C), y(C)+random()*Longitud(f)/2-Longitud(f)/4)
per dibuixar un punt P a la posició d’un punt C però a diferent alçada (segons un segment f):
x(C): s’usa per obtenir la coordenada x del punt C;y(C): s’usa per obtenir la coordenada y del punt Crandom(): genera un nombre aleatori entre 0 i 1, que podem multiplicar per la longitud de la meitat d’un segment*Longitud(f)/2perquè estigui entre 0 i la longitud de mig segment.-Longitud(f)/4: en restar-li una quarta part de la longitud del segment, el nombre aleatori acabarà entre -1/4 part i +1/4 part de manera que tant pot estar per sobre com per sota (pujar o baixar).
Applet perquè facis tu la construcció:
Prova de fer-ho sense pistes (però si necessites ajuda, fes una ullada a aquest document):
Ara pots provar com seria en 3D amb aquesta eina:
Fons d'informació i imatges:
Min-Fang Grace Tsai, Fractal landscapes, 2003
- https://www.sfu.ca/~rpyke/335/projects/tsai/report1.htm
64bitdragon, Midpoint Displacement in one dimension
- https://learn.64bitdragon.com/articles/computer-science/procedural-generation/midpoint-displacement-in-one-dimension
Bites of code, Landscape generation using midpoint displacement, 2016
- https://bitesofcode.wordpress.com/2016/12/23/landscape-
generation-using-midpoint-displacement/
The craft of coding, Midpoint displacement algorithm
- https://craftofcoding.wordpress.com/tag/midpoint-displacement-algorithm/