E13 Egy KöMaL feladat, és ami mögötte van....
A KöMaL 2021. februári számában megjelent B.5153 számú feladat, amelyet Tarcsay Tamás, valamint e sorok írója tűzött ki, ez volt:
Legyenek A, B, C egy egységnyi oldalú szabályos háromszög csúcsai, míg D egy pont az AB oldal B-n túli meghosszabbításán. A BC szakaszra B-ben állított merőleges a CD szakaszt az E pontban metszi.
Határozzuk meg a CE szakasz hosszát, ha ED=1
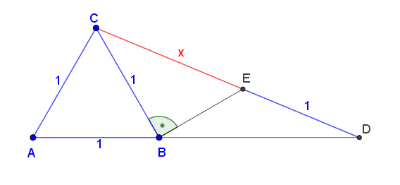
Amellett hogy mutatunk e feladatra néhány megoldást, meg szeretnénk ismertetni olvasóinkat a feladat több, mint kétezer éves hátterével is.
A feladat (egy) elemi megoldása
A gyakorlott feladatmegoldók fejében e feladat láttán bizonyára azonnal felmerülnek Pólya György klasszikus kérdései:
- Hogyan tudnánk kapcsolatot teremteni az adatok és az ismeretlen között?
- Hogyan használhatnánk ki, hogy az ABCΔ szabályos?
- Melyek az ábra ismert szögei?
- Általában milyen összefüggések vezethetnek egy geometria feladat ismert és ismeretlen szakaszai közötti kapcsolat felderítéséhez?
- Vannak-e hasonló háromszögek a feladat ábráján? Ha nincsenek, ki tudnánk-e egészíteni a rajzunkat úgy, hogy legyenek?
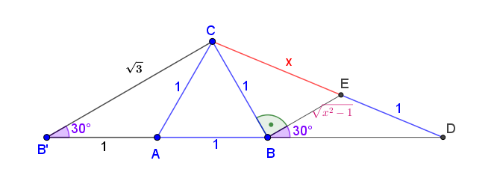
- Egészítsük ki az ábránkat a B pont A-ra vonatkozó tükörképével. Legyen ez B'!
- Vegyük észre, hogy B'C ∥ BE, mivel DBE ∢ =DB'C ∢ =30°!
- Így ezért
. - Másrészt, mivel CAB'∢ =120° , így , és EBC∢ =90° , ezért . Ezek alapján: , ebből: .
- Az egyenletet szorzattá alakítva: , vagyis .
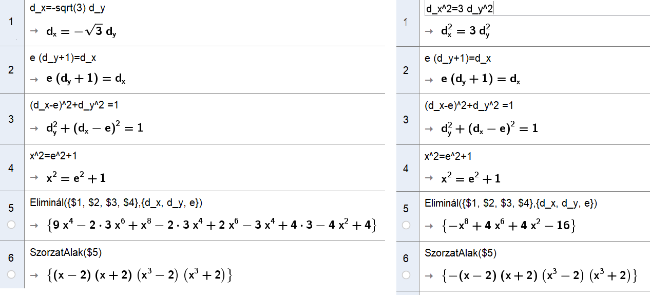
A feladat megoldása a GeoGebra CAS rendszerével.
Játsszunk el azzal az ötlettel, hogy nem volt ötletük a fenti - elegáns(??) - megoldáshoz. Rá tudnánk bízni ezt ez egész problémát a GeoGebrára? Végül is - megfelelő előkészítés és a GeoGebra CAS rendszer alapos ismeretének a birtokában - igen.
Előkészítés
Általában igaz, hogy ha egy geometria feladat megoldásakor - jobb híján - az analitikus utat választjuk, akkor számítanunk kell arra, hogy ez alaposabb szakmai felkészültséget, és a legtöbbször sok számolást igényel. Azonban azzal, hogy körültekintő módon helyezzük koordinátarendszerbe a feladatunkat, és jól előkészítjük a számolási részt, sokat javíthatunk a helyzetünkön. Ha a számolást valamilyen CAS rendszerre szeretnénk bízni, ez talán még fontosabb része a munkának.
Legyen B=(0,0) , C=(0,1), D=(dx,dy) és E=(e,0). A koordináták ilyen megválasztása mellett máris kihasználtuk a CB⟂BE feltételt.
Elemezzük rendre a GeoGerának adott CAS parancsokat:
- A DBE∢=30° feltételt a dx és dy közötti kapcsolattal fejeztük ki, mindjárt két különböző módon felírva. (Így az A pontra nincs is szükségünk.) Figyeljük meg, hogy elkerülve az irracionális együtthatót, mennyivel "szelídebbek" lettek annak a polinomnak az együtthatói, amelynek a zérushelyei között ott van a keresett eredmény is.
- Így - szorzat alakban felírva - fejeztük ki hogy a C, E és D pontok kollineárisak.
- Felírtuk az ED=1 feltételt.
- Felírtuk a keresett x = CE kapcsolatot.
- A Geogebra talán kevésbé ismert Eliminál() parancsával kiküszöböltük a számunkra érdektelen változókat. *
- Az így kapott első pillanatra ijesztő 8-adfokú polinom szorzattá alakítható, ebből már leolvasható a keresett x érték.
Elemi trigonometriai összefüggéseken alapuló megoldásra is gondolhatunk.*
Az x=CE szakasz mellett legyen y=BE és z=BD. Mivel az összes B csúcsú szög ismert, felíratjuk a BCEΔ-re a Pitagorasz tételt, BCDΔ és BEDΔ -re a koszinusz tételt.
Az így kapott háromismeretlenes egyenletrendszer láttán legtöbben leteszik a tollat, hiszen innen a matematika nem szép része következne. De manapság a CAS rendszerek többnyire - így most is - elvégzik helyettünk ezt a munkát. Ebből már csak ki kell választani a geometriai tartalomhoz tartozó megoldást:
*Köszönjük Dr. Hujter Mihálynak, ezt a megoldást, Tarcsay Tamásnak az egyenletrendszer CAS megoldását.
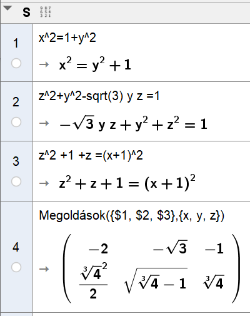
A déloszi probléma
A matematikatörténetben valamelyest tájékozott olvasóink bizonyára felismerték, hogy a feladat megoldásaként kapott szám a híres ókori szerkesztési problémák egyike, a déloszi probléma.
A történet röviden: Délosz szigetén kitört a pestis járvány. Megfékezésére az orákulum azt javasolta, hogy cseréljék ki a sziget Apolló szobrának a kocka alakú talapzatát egy kétszer akkora térfogatú kockára. A kérdés az volt, hogy ennek az élhossza megszerkesztető-e az euklideszi eszközökkel az egységnyi szakaszból.
Ez - a többi híres ókori szerkeszthetőségi problémával együtt - 1837-ig nyitva maradt, amikor Pierre Wantzel igazolta, hogy a feladat euklideszi szerkesztéssel nem oldható meg. Annak ellenére , hogy addig is sokakat foglalkoztattak ezek a kérdések, Wantzel eredménye még legalább ötven évig nem jutott el a matematikai köztudatba. Épp úgy, mint ahogy Bolyai János geometriai munkásságát is ötven év elteltével ismerte meg a világ.
Bár az ókori görög matematikusok nem tudták megoldani a déloszi problémát, találtak rá egy -áthidaló - megoldást. Kitaláltak egy a GeoGebra szempontjából is figyelemre méltó eszközt, a neuszisz vonalzót (vagy neuszisz körzőt?), amellyel jórészt megoldhatóvá váltak a híres ókori szerkesztési problémák. Ezzel a témakörrel már csak az ókori görög matematikusok iránt érzett tiszteletből is - érdemes megismerkednünk. Itt mutatjuk be az erről készült GeoGebra anyagunkat.
Végül is a járvány elmúlt, mint utóbb kiderült, az istenek nem is akarták, hogy ezt a problémát megoldja az emberiség, csak ezzel kívánták az emberek figyelmét a geometria irányába terelni. Sikerült.
Mi is erre törekedve javasoltuk kitűzésre a fenti feladatot, amely lényegében Nikomédész szerkesztésén alapszik.