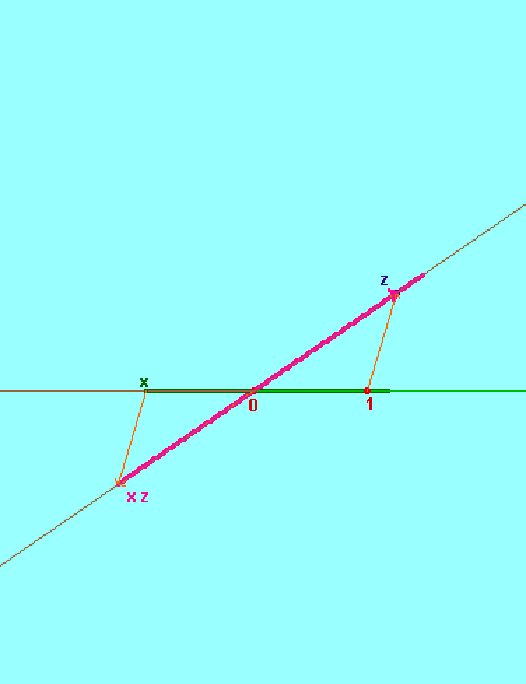
Ottenere rette, semirette e segmenti da R
parametrizzazione di una retta
- operatore di parametrizzazione di retta (moltiplicando fisso): se si fissa un punto z, la funzione da R a C definita dalla corrispondenza x
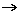x•z è detta parametrizzazione lineare che porta 1 in z. Ponendo Lz(x) = x•z, si ottiene la notazione Lz per tale parametrizzazione lineare.
L'insieme Lz(R) = {Lz(x) : x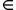
R} = {x•z : x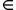R} è detto retta passante per l'origine e per z, e si indica brevemente con R•z o semplicemente con Rz. Per tale motivo Lz è detta parametrizzazione di Rz. E' proprio questo operatore che giustifica la denominazione di "moltiplicazione lineare"
- proprietà delle parametrizzazioni lineari (immediatamente deducibili dalla definizione):
- origine fissa: Lz(0) = 0
- corrispondente dell'uno uguale al moltiplicando: Lz(1)=z
- linearità: Lz(x+y) = Lz(x) + Lz(y) e Lz( r·x) = r·Lz(x)
- corrispondenza biunivoca fra R e Rz: Lz è una funzione iniettiva dall'asse reale R sulla retta Rz, quindi è una bijezione fra R e Rz.
