características de la función a trozos
Normalmente, las funciones (con una variable x) se definen con una única expresión algebraica, por ejemplo,
f(x)=3x2−1xf(x)=3x2−1x
y la variable x toma valores reales (excepto aquellos que son problemáticos, como los que anulan el denominador).
Las funciones seccionadas, segmentadas o definidas por partes o a trozos, son funciones que se definen de un modo u otro según el valor que toma la variable xx. Veamos un ejemplo:
Ejemplo:
f(x)={2x+1si x≤0x2si x>0f(x)={2x+1si x≤0x2si x>0
En esta función, si la variable toma un valor menor o igual que 0, la definición de la función es 2x+12x+1, mientras que si toma un valor positivo la definición de la función es x2x2.
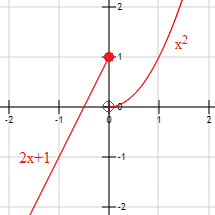El punto sólido y el punto vacío de la gráfica indican que el valor que toma f en x=0x=0 es f(0)=1f(0)=1 y no f(0)=0f(0)=0 (porque x=0x=0 pertenece al primer intervalo de la definición de f).
CARACTERÍSTICAS:
Su dominio son los R
Su función es discontinua en x=1
La función es decreciente desde [-∞,0) y creciente desde (0,+∞)
tiene un mínimo en x=0
intersecta a los ejes en= (0,0)
El punto sólido y el punto vacío de la gráfica indican que el valor que toma f en x=0x=0 es f(0)=1f(0)=1 y no f(0)=0f(0)=0 (porque x=0x=0 pertenece al primer intervalo de la definición de f).
CARACTERÍSTICAS:
Su dominio son los R
Su función es discontinua en x=1
La función es decreciente desde [-∞,0) y creciente desde (0,+∞)
tiene un mínimo en x=0
intersecta a los ejes en= (0,0)