… aus Durchhang u. Pfeilerabstand
III. Ermitteln der Funktion (Teil 1)
… aus Durchhang und Pfeilerabstand
Gegebene Daten
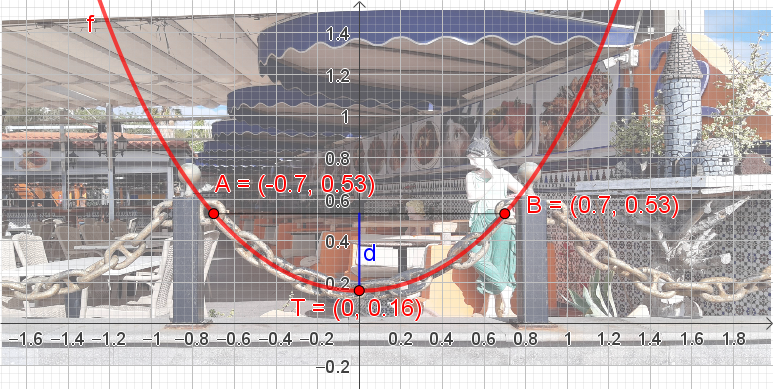
Die Aufhängepunkte der Kette seien und , im Beispiel mit den Werten und .
Der tiefste Punkt der Kette möge um tiefer liegen als die Aufhängepunkte („Durchhang“).
Im Bild befindet sich der Tiefpunkt auf der y-Achse ungefähr bei 0.16.
Er liegt damit um tiefer als die Aufhängepunkte.
.
Gleichung für den Formparameter a
Die Funktion soll an der Stelle x=0 den Wert h-d haben:
Wegen folgt
oder
.
Mit der Gleichung (VI) aus Kapitel II. Mathematischen Grundlagen wird die Formel zu
.
Der Parameter a für die Form der Kettenlinie ist also nur durch den Wert von c (halber Abstand der Pfeiler) und den Wert d (Durchhang der Kette) festgelegt.
Mit den Werten von oben, nämlich c=0.7 und d=0.37, gilt:
.
Diese Gleichung lässt sich nicht nach a auflösen.
Aber mit einem geeigneten Taschenrechner oder mit GeoGebra lässt sich eine Lösung für diese Gleichung finden.
Bestimmung von a mit dem CAS-Modul von GeoGebra
Hier sind nur zwei Zeilen zu schreiben:
In der zweiten Zeile wird die Anweisung NLösungen für numerisches Lösen verwendet.
Dabei wird $1 als Platzhalter für die zu lösenden Gleichung angeben.
Der passende Wert für a ergibt sich dann mit .
Machen wir uns nichts vor: solange der Abstand 2c1,4m und der Durchhang d0,37m nicht genauer gemessen werden, ergibt es keinen Sinn, den Parameter a auf eine Genauigkeit von 5 Stellen zu bestimmen.
Der Wert stimmt mit dem aus der Schieberegler-Methode von der vorigen Seite gut überein.
Dort sehe ich die beste Übereinstimmung von Kurve und Kette bei a=0,715 oder a=0,72.
Der Operator NLösungen ist hier besser als NLöse geeignet, weil dass das Ergebnis dann eine einfache Menge ist.
Für das Zeichnen der Funktion
kann im Algebrafenster auf den berechneten Wert zugegriffen werden, indem mit
a = Element(L,1)
das erste (und in diesem Fall: einzige) Element aus der Lösungsmenge herausgeholt wird.