3. Luthiers
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
La onda
Otra forma de recoger la información del timbre es mediante la gráfica de la onda sonora, es decir, de la serie de Fourier (ver el artículo "Análisis Armónico") correspondiente a la suma baremada, según su intensidad, de todos esos sonidos parciales.
Veamos la onda del diapasón:
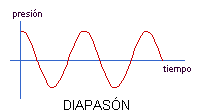
Su sencilla forma senoidal refleja la sencillez de su composición. Se trata de prácticamente un único sonido fundamental, sin parciales apreciables.
Comparemos la gráfica anterior con la correspondiente a una trompeta:
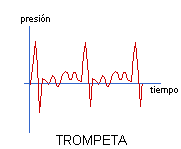
La presencia de varios armónicos complica la gráfica, provocando crestas e irregularidades. Veamos ahora la gráfica de un clarinete:
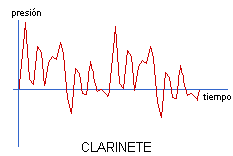
Podemos apreciar que ahora la distribución de armónicos es todavía más compleja. Esa riqueza de matices muestra al clarinete como más próximo a la voz humana, más “cálido” o “íntimo”, bajo nuestra percepción.
Luthiers
En el artículo Prehistoria musical, aparece:
Las combinaciones de vibraciones componen el timbre de cada instrumento. En la creación de los instrumentos se resaltan aquellos armónicos naturales que le confieren timbre propio. La misión principal de un luthier es justamente dotar al instrumento del timbre que se espera de él.
Sirva la mención al luthier como excusa para mencionar a aquellos que “unen canto con humor”, el grupo argentino autor de una de las escasísimas canciones dedicadas expresamente a las matemáticas: el divertimento matemático opus 48, Teorema de Thales, plagio milimétrico de la obra del mismo nombre del casi siempre impresentable compositor Johann Sebastian Mastropiero. Pulsando sobre las siguientes imágenes podemos oír una frase musical de esta obra y el sonido de uno de los originales instrumentos creados por Les Luthiers.
| Dada la enorme cantidad de vibraciones que simultáneamente pueden incidir en nuestro tímpano, haciéndolo vibrar a su vez, hemos desarrollado un complejo sistema discriminatorio, capaz de “separar” la combinación recibida en “partes más simples”. Este sistema se basa en la disposición, en el oído interno, de células especializadas en activarse sólo ante determinadas frecuencias, al estar situadas en medios que sólo entrarán en resonancia en esas frecuencias. Simplifiquemos un poco en aras de mayor claridad. Nuestro oído puede percibir vibraciones con frecuencias comprendidas entre unos 18 Hz y unos 18.000 Hz. Si percibimos un sonido resultado de la combinación de cuatro vibraciones: sonido={200, 708, 1.524, 3.967}, las células especializadas en la recepción de cada tipo de vibración cribarán las componentes del sonido: solo se activarán las células situadas en zonas que entren en resonancia con las frecuencias 200, 708, 1.524 y 3.967. Al sonido percibido lo podemos llamar “200-708-1.524-3.967”, pero es muy importante para la comprensión de la relación entre música y matemáticas tener en cuenta desde un principio que registramos cada frecuencia por separado. Cuantas menos vibraciones compongan un sonido, menos actividad se registrará en nuestro oído. Nuestra percepción mental es de un sonido “puro”, “claro”, “nítido”. El sonido producido por un diapasón es un buen ejemplo. Su equivalente visual podría ser un cielo despejado. Por el contrario, si son muchas y de diverso tipo las vibraciones que conforman el sonido, percibiremos éste como “oscuro”, “confuso”, “impreciso”. Su equivalente visual podría ser un tupido bosque. Además, aunque en principio la intensidad del sonido es independiente de la frecuencia, no lo es en nuestra recepción del sonido. Nuestro oído es más sensible a las altas frecuencias, de forma que con la misma intensidad de sonido percibimos un volumen mayor en frecuencias altas respecto a las bajas. |