n=30 Icosidodecahedron. Images: A critical points scheme for Generating uniformly distributed points on a sphere.
The applet illustrates the case where 30 vertices of a Icosidodecahedron "induce" the vertices of two other polyhedra:
V=32 ●Pentakis Dodecahedron← V=30 ●Icosidodecahedron →V=60 ☐Rhombicosidodecahedron.
Generating polyhedra is in https://www.geogebra.org/m/hymcebuw. Description are in https://www.geogebra.org/m/y8dnkeuu and https://www.geogebra.org/m/rkpxwceh.
![[size=85]A system of points on a sphere S of radius R “induces” on the sphere S0 of radius R0 three different sets of points, which are [color=#93c47d]geometric medians (GM)[/color] -local [color=#ff0000]maxima[/color], [color=#6d9eeb]minima[/color] and [color=#38761d]saddle[/color] points sum of distance function f(x). The angular coordinates of the spherical distribution of a system of points -[color=#0000ff] local minima[/color] coincide with the original system of points.[/size]](https://www.geogebra.org/resource/ankbj8xg/URqa3MjNGOmRTJ8I/material-ankbj8xg.png)
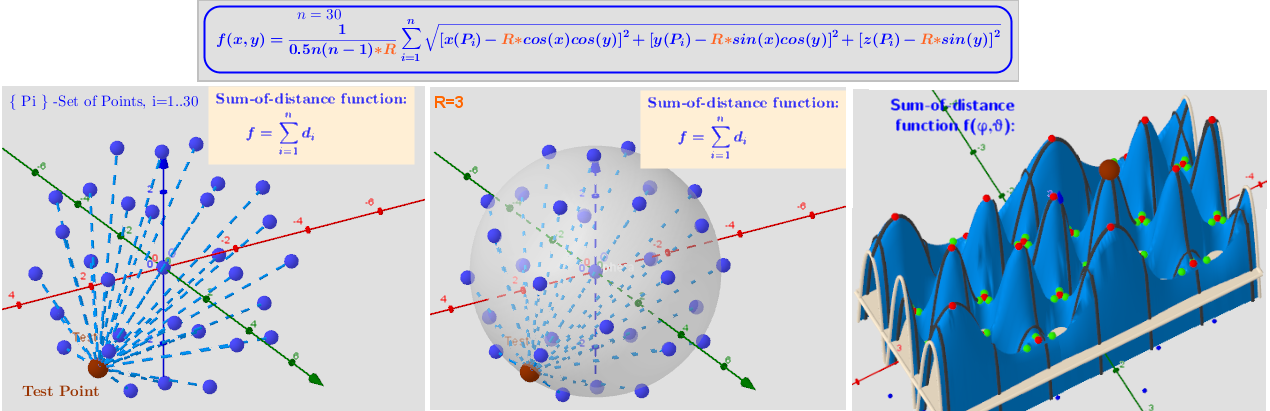
![[color=#333333]Distribution of points Pi[/color][color=#ff0000], [color=#5b0f00]test Point[/color], [color=#ff0000]Max[/color]/[color=#0000ff]min[/color]/[color=#38761d]saddle[/color] -[color=#333333]Critical points[/color] on a sphere. Vectors ∇f and ∇g at these points.
max:[/color] Pentakis Dodecahedron
[color=#0000ff]min:[/color] Icosidodecahedron
[color=#6aa84f]sad:[/color] Rhombicosidodecahedron(c)](https://www.geogebra.org/resource/h2qbawan/WRRqWaWShEkgEFpB/material-h2qbawan.png)
![[size=85][color=#ff0000]max:[/color] Pentakis Dodecahedron
[color=#0000ff]min:[/color] Icosidodecahedron
[color=#6aa84f]sad:[/color] Rhombicosidodecahedron(c)[/size]](https://www.geogebra.org/resource/fktn5ct8/4mEjQqFoSNOSFRm8/material-fktn5ct8.png)
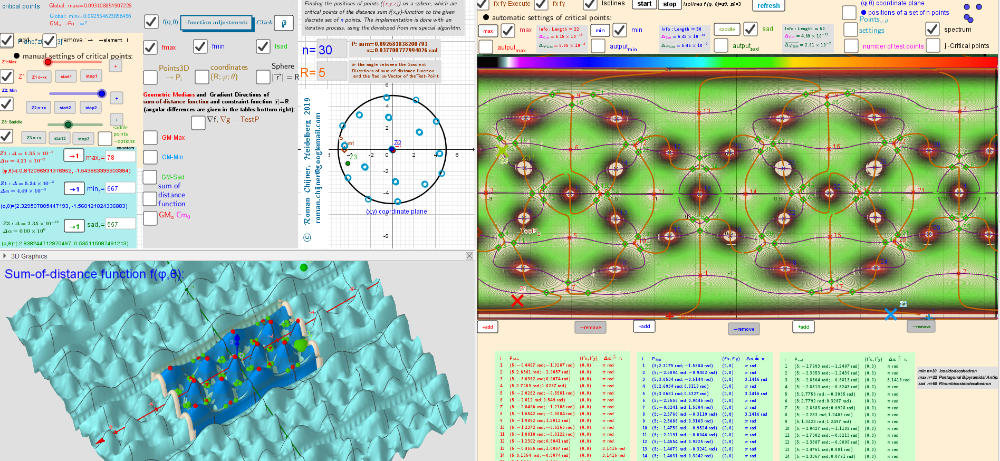
Isolines
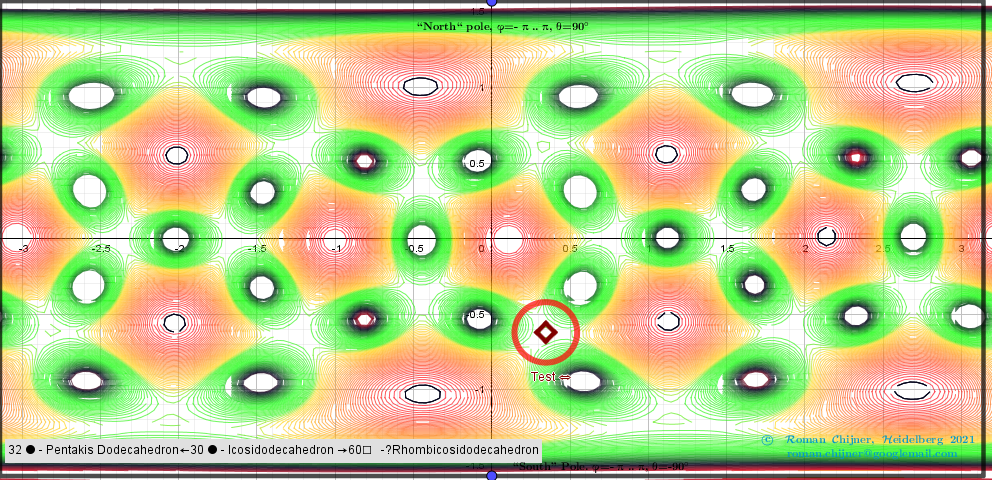
![[size=85]Intersection points of implicit functions over a rectangular region: - π ≤φ ≤ π; -π/2≤θ≤π/2. A [color=#980000][b]Test[/b][/color] [b][color=#980000]point[/color][/b] -color indicator of the critical point [/size]](https://www.geogebra.org/resource/thgaq7ts/z3mj28LPmuRngYM2/material-thgaq7ts.png)
![[size=85]Isolines and Intersection points of implicit functions over a rectangular region: - π ≤φ ≤ π; -π/2≤θ≤π/2.[/size]](https://www.geogebra.org/resource/sme9pnzm/qKapPMp02MGDkMZV/material-sme9pnzm.png)
![Automatic calculation of critical: [color=#ff0000]max[/color], [color=#0000ff]min[/color], [color=#6aa84f]saddle[/color] points -Solutions of the Lagrange equations.](https://www.geogebra.org/resource/ungfa9k8/wYXGycM5naCMm8Yg/material-ungfa9k8.png)