Das RSA-Verfahren
Ein schwieriges Problem
Betrachten wir noch mal die Situation von Alice, Bob und Eva. Die bisherigen Schlüsselverfahren verlangten , dass Alice und Bob den gleichen Schlüssel haben. Das heißt, sowohl bei der Caesar- als auch bei der Vigenère-Verfahren als auch beimDiffie-Hellman Verfahren müssen alle Kommunikationspartner den gleichen Schlüssel kennen. Dies stellt doch manchmal ein Problem dar, überlege dir warum ?
Was nun?
Die Lösung heißt asymmetrische Verschlüsselung.
Die asymmetrische Verschlüsselung basiert darauf, dass beide Kommunikationspartner einen öffentlichen und einen privaten Schlüssel
verwenden.
Dabei muss der öffentliche Schlüssel sich mittels Einwegfunktion
berechnen lassen und dieser Schlüssel darf publik gemacht werden.
Zusätzlich muss der private Schlüssel geheim gehalten werden.Die
verschlüsselte Nachricht ist dann eine Kombination aus geheimen
Schlüssel des Senders als auch öffentlichen Schlüssel des Senders ,sowie
die zu verschlüsselnde Klartextnachricht.
Dabei dürfen öffentliche Schlüssel und die verschlüsselte Nachricht in
die Hände dritter, in unserem Fall Eva gelangen.
Ein sehr modernes und bekanntes Verfahren ist deshalb das RSA
Verfahren, das auf der asymmetrischen Verschlüsselung basiert.
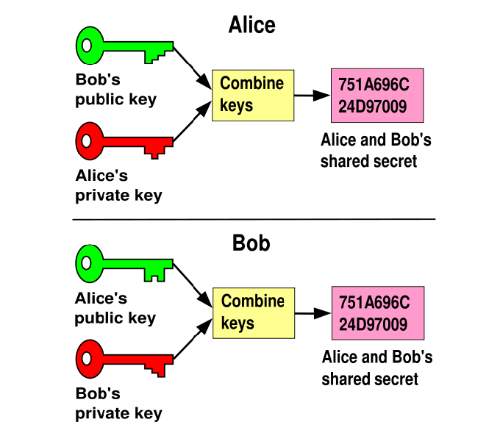
Folgendes Schaubild soll die Schlüsselerzeugung demonstrieren:
Schaubild zur Schlüsselerzeugung
Wie funktioniert die Schlüsselerzeugung?
Die Schlüsselerzeugung funktioniert in 3 Schritten:
1. Man wählt zwei Primzahlen und . Beachte aber, dass diese beiden Primzahlen sollen möglichst groß gewählt werden.
2. Dann berechnet man und
3. Dann wählt man zwei natürliche Zahlen und , sodass der größte gemeinsame Teiler und gilt.
Zusammenfassend ist der privaten Schlüssel, und bilden den öffentlichen Schlüssel.
Des Weiteren sind und möglichst vernichtet werden.
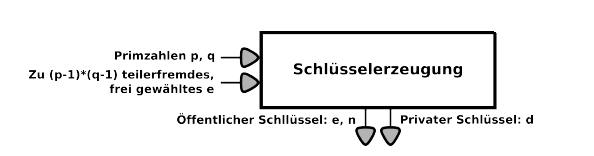
Ein weiteres Schaubild zu Visualisierung sollte helfen:
Schaubild Schlüsselerzeugung Algorithmus
Beispielhafte Berechnung
Wähle und .
Dann gilt
.
Des Weitern bestimme ich
.
Wir wählen nun und überprüfen, ob e teilerfremd zu ist. Dazu gebrauchen wir den erweiterten euklidischen Algorithmus.
Daraus folgt, dass und teilerfremd sind.
Nun bestimmen wir mittels Bézout-Koeffizienten das .
Dabei ist der Koeffizient vor der das zu suchende . Also .
Aufgabe 1
Berechne für und den Teil des öffentlichen Schlüssels und den geheimen Schlüssel .
Aufgabe 2
Berechne für und den Teil des öffentlichen Schlüssels und den geheimen Schlüssel .
Ver- und Entschlüsselung
Möchte man nun konkrete Nachrichten verschlüsseln, gelingt dies wie
folgt:
Wie verwenden nun die öffentlichen Schlüssel unseres Kommunikationspartners . Dann nehmen wir ein Klartext in den natürlichen Zahlen und dieser kann wie folgt verschlüsselt werden:
Unser Kommunikationspartner erhält dann die verschlüsselte
Nachricht und kann diese wie folgt entschlüsseln:
Formel zu Verschlüsselung:
Unser Kommunikationspartner entschlüsselt dann die Nachricht wie folgt:
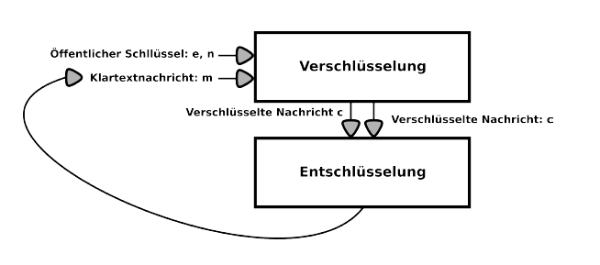
Folgendes Schaubild illustriert dies ganz gut:
Schaubild Ver- und Entschlüsselung
Aufgabe 3
Verschlüssele die Nachricht mit und und gib das resultierende an.
Aufgabe 4
Entschlüssele die Nachricht mit und und gib das resultierende an.