Schritt 1: Differenzenquotient - Lupe
Schritt 1: Von der Sekante zur Tangente
Wir betrachten die Funktion .
Auf dem Graphen von f liegen die Punkte P(1|f(1)) und Q(2|f(2)).
Nachdenken...
Was sind die Koordinaten von P und Q?
Nachdenken...
Welche Steigung hat die Sekante durch die Punkte P und Q?
Wir betrachten nun was passiert, wenn wir den Punkt Q entlang des Graphen auf den Punkt P zubewegen. Betrachte dazu das folgende Applet. Mit dem Schieberegler kannst du den Wert von h verändern. Je kleiner h ist, desto näher liegt Q an P.
Ein Blick auf den Graphen - von der Sekante zur Tangente
Im Heft:
Fertige einen Screenshot für h=1 an und füge ihn in dein Heft ein.
Finde durch Veränderung am Schieberegler folgende Sekantensteigungen und notiere sie in einer Tabelle im Heft:
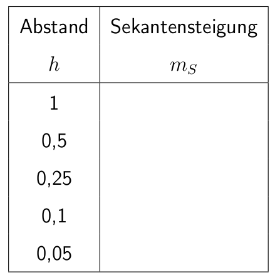
Kontrolle
Welchen Wert hat die Sekantensteigung für h=0,1?
Tangentensteigung
Wählst du h=0, so liegt Q auf P. Aus der Sekante (die den Graphen in zwei Punkten schneidet) ist eine Tangente geworden, die den Graphen an der Stelle P berührt. Die Tangente schmiegt sich an den Graphen an, so dass die Steigung der Tangente gleich der Steigung des Graphen an der Stelle x=1 ist.
Wir bestimmen also den Grenzwert des Differenzenquotienten:
Um mathematisch auszudrücken, dass h immer kleiner wurde, verwenden wir den Begriff des Grenzwertes:
(lies: Limes für h gegen 0) bedeutet, dass wir den Grenzwert bilden, wenn h immer kleiner wird.
Ergebnis
Schreibt folgenden Merksatz in euer Heft:
Die Steigung eines Graphen an einer Stelle kann über die Tangentensteigung bestimmt werden. Sie kann mit dem Grenzwert des Differenzenquotienten berechnet werden und wird als Ableitung an der Stelle bezeichnet:
Nachdenken...
Einen Grenzwert zu bilden klingt kompliziert. Wieso kannst du im Differenzenquotient nicht einfach für h den Wert 0 einsetzen?
Beispiel
Oben hast du für die Funktion die Tangentensteigung an der Stelle bestimmt. Die Tangentensteigung und damit die Steigung des Graphen ist an dieser Stelle 1.
Wir schreiben:
(lies: Die Ableitung von f an der Stelle ist 1.
Aufgabe
Was bedeutet der Ausdruck ?