Teorema de Tales
Teorema de Tales
El Teorema de Thales es un concepto fundamental en la geometría que nos ayuda a comprender las propiedades de las figuras geométricas y las relaciones entre sus elementos. Este teorema establece una conexión entre las líneas paralelas y los triángulos semejantes, y su aplicación se extiende a una amplia variedad de problemas geométricos.
En los siguientes ejercicios, exploraremos cómo aplicar el Teorema de Thales para resolver problemas prácticos y demostrar sus propiedades en situaciones del mundo real. A través de estos ejercicios, desarrollaremos una comprensión más profunda de este importante teorema y su relevancia en la resolución de problemas geométricos cotidianos.
Ejemplo el teorema de Tales para entender mejor, observemos la siguiente figura:
Por el teorema de Tales se puede concluir que α=δ y β=εAdemás, como mencionamos previamente, los lados son proporcionales, por lo que se cumple que :
Ejercicio 1 Las rectas a y b del dibujo son paralelas. Comprueba utilizando el teorema de Tales si también lo es la recta c.
¿Cómo demostramos que la recta c es paralela?Pues tenemos que demostrar que las rectas están en posición de Tales y que se cumple el teorema de Tales, comprobando si los segmentos de ambas rectas tienen la misma razón y que entre ellas sean proporcionales.Calculamos la razón de los primeros segmentos:
Y la razón de los siguientes dos segmentos:
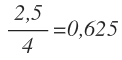La razón es la misma, por lo que ambos pares de segmentos son proporcionales.Entonces se cumple el teorema de Tales y como consecuencia, la recta c es paralela.