Section 10.2 Activities
Part A: Linear Angles
#1
Using the locationof the two angles to write a definition for a linear angle pair.
#2
What do you observe about the angle measures of the linear angle pair?
#3
Make a conjecture about the sum of the measures of anylinear angle pair.
Part B: Vertical Angles
#4
Based on the location of one of the vertical angle pairs above, write a definition for a vertical angle pair.
#5
Use points A, B, C, and D to change the angle values. Make a conjecture about the measures of a pair of vertical angles.
Part C: Additional Angle Pairs
#6
Move one of the lines by dragging one of the points on the line. Notice that the pairs stay the same (the colors don’t change). When do the angle pairs seem the most equal in size?
#7
Now, use the slider at the top of the screen to highlight some differentangle pairs. (Not corresponding angles, but different angle pairs.) Define these pairs based on their location with respect to the transversal.
Part D: The Parallel Postulate
#8
What are the colored angled pairs called?
#9
What do you notice about the angle measures of the angle pairs?
#10
Fill in the blanks below to define the Parallel Postulate: Parallel Postulate: When two ________________________ lines are cut by a _________________________________, the resulting __________________________________ angles are ______________________.
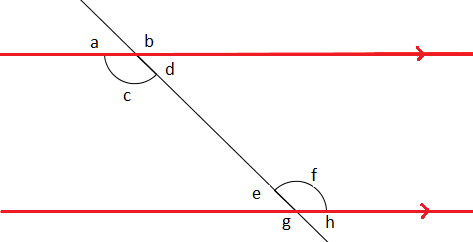
#11
Use the Parallel Postulate to prove that if two parallel lines are cut by a transversal, then the alternate interior angles are congruent. (That is, c=f in the diagram above.)
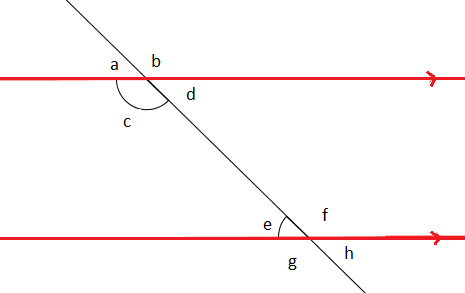
#12
Use the Parallel Postulate to prove that if two parallel lines are cut by a transversal, then same side interior angles are supplementary. (That is, c+e = 180 in the figure above.)