2 Chancen und Risiken digitaler Werkzeuge
Wir leben in einer Gesellschaft, in der die Digitalisierung immer mehr an Relevanz gewinnt.
Deshalb sollen digitale Medien auch immer mehr Einzug in die Bildung finden, beispielsweise durch digitale Werkzeuge in den Fachunterrichten, so auch im Mathematikunterricht. Dadurch tragen wir einen Teil zur allgemeinen Medienkompetenz der Schülerinnen und Schüler bei.
Digitale Werkzeuge bringen eine Vielzahl an Chancen und Möglichkeiten mit sich, birgen aber auch Risiken.
Beide Aspekte werden im Folgenden näher erläutert.

Zentrale Potenziale digitaler Werkzeuge (nach Thurm)
Wir beschäftigen uns zunächst mit zwei der vier zentralen Potenziale digitaler Werkzeuge nach Thurm.
Zu Beginn befassen wir uns mit dem Aspekt der "Unterstützung von Modellierungsprozessen".
Der Begriff Modellieren
Modellieren bedeutet
Komplexe und realistische Fragestellungen mithilfe von Mathematik zu lösen (primakom Deutsches Zentrum für Lehrkräftebildung Mathematik) Die Bedeutung von Modellieren ist daran ersichtlich, dass dies als eine der prozessbezogenen Kompetenzen im Bildungsplan Baden-Württemberg für das Fach Mathematik verankert ist. Laut diesem sollen die Schülerinnen und Schüler "Realsituationen analysieren und aufbereiten", "mathematisieren", "im mathematischen Modell arbeiten" und "interpretieren und validieren" können. (vgl. Kultusministerium: Gymnasium - Mathematik. Bildungspläne Baden-Württemberg. Online verfügbar unter https://www.bildungsplaene-bw.de/,Lde/LS/BP2016BW/ALLG/GYM/M, zuletzt geprüft am 24.10.2022.) Der Modellierungskreislauf nach Blum und Leiß Blum und Leiß entwickelten einen siebenschrittigen Modellierungskreislauf, um die einzelnen Teilprozesse des Modellierens zu beleuchten.
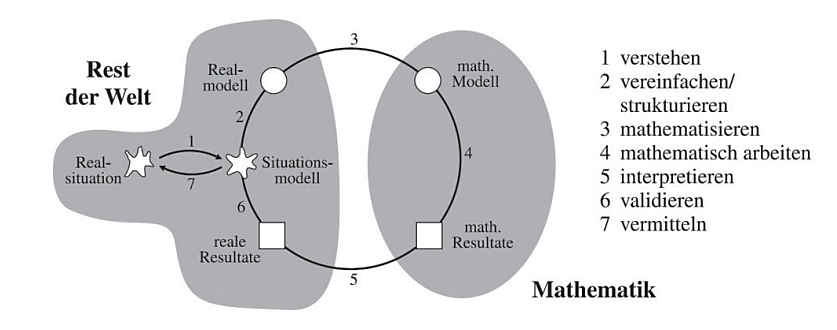
Digitale Werkzeuge werden als große Chance verstanden den Modellierungsprozess zu unterstützen. So kann zum einen mit größeren Datenmengen gearbeitet werden und zum anderen können Aufgaben mit aufwendigeren Berechnungen gelöst werden. Somit kann auch der Realitätsbezug der Aufgaben zunehmen.
Ein weiteres Potenzial digitaler Werkzeuge beschreibt die "Entlastung von kalkülhaftem Arbeiten".
Entlastung von kalkülhaftem Arbeiten
Zunächst betrachten wir den Begriff Wissen genauer. Wissen teilt sich zum einen in das konzeptuelles Wissen, also dem inhaltlichen Verständnis und zum anderen in das prozedurale Wissen, dem Wissen um die Durchführung von Rechenoperationen.
Aus der Sicht der Wissenschaft sind zum Erreichen mathematischer Kompetenzen beide Wissensformen gleichermaßen wichtig, aber leider wird in der Praxis der Fokus häufig nur auf das prozedurale Wissen gelegt und das konzeptuelle Wissen außer Acht gelassen.
In diesem Kontext bietet der Einsatz digitaler Werkzeuge folgende Chancen und Risiken:
| Chancen | Risiken |
| Operative Rechentätigkeiten können ausgelagert werden und somit kann der Fokus stärker auf die Interpretation und Reflexion von Sachverhalten gelegt werden Rechtfertigung: nachlassende Relevanz von operativen Tätigkeiten | die ausgegebenen Ergebnisse des digitalen Mediums werden stumpf übernommen Operative Rechentätigkeiten gehen verloren oder werden nicht ausgebildet Mathematische Konzepte werden nicht (mehr) verstanden Vermeidung von Mathematik |
Die Wirksamkeit von digitalen Werkzeugen im Mathematikunterricht
Leider gibt es trotz zahlreicher Studien keine eindeutige Antwort auf die Frage wie wirksam der Einsatz digitaler Werkzeuge im Mathematikunterricht ist. Das liegt zum einen an mangelnder Vergleichbarkeit der Studien und andererseits an methodische Schwächen dieser. Außerdem lässt sich ein Lernerfolg nicht einzig auf den Einsatz digitaler Werkzeuge zurückführen.
Der allgemeine Konsens der Wissenschaft ist aber, dass für die Wirksamkeit entscheidend ist wie das digitale Werkzeug in den Unterricht eingebettet wird und welche Ziele verfolgt werden. Somit kommt hierbei der Lehrkraft eine zentrale Rolle zu.
Unterrichtspraxis - Medienkompetenzmodell nach Pallack
Unter Medienkompetenz wird die Bereitschaft und Fähigkeit verstanden, zeitgemäßes medienbezogenes Wissen und Können zur Lösung von Problemen anwenden zu können.(Pallack, A. (2018): Digitale Medien im Mathematikunterricht der Sekundarstufen I + II, S.46), Das von Pallack entwickelte Medienkompetenzmodell dient zur Einschätzung der eigenen Medienkompetenz, sowohl für Lehrende als auch für Lernende. Diese ist ein entscheidender Faktor für die Unterrichtsplanung, -durchführung und -reflexion. Das Modell ist vierstufig mit aufeinander aufbauenden Ebenen (hier von unten nach oben).
| Lernende | Lehrende |
| Reflexion über die Nutzung des digitalen Mediums | Reflexion: Erfahrungen zum Einsatz, Chancen und Risiken, Konsequenzen auf eigenes pädagogisches Handeln |
| Eigenständige Nutzung des digitalen Mediums | Einsatzmöglichkeiten im Hinblick auf das Lernen von Mathematik |
| Bedienung des digitalen Mediums | Wissen über die technischen Nutzung und der Funktionen |
| Wissen über das digitale Medium | Wissen über zentrale Informationen, Einsatzmöglichkeiten und Zielsetzungen des digitalen Mediums |
Fazit
Digitale Werkzeuge bringen große Potentiale mit sich und können beispielsweise dabei helfen den
Lernprozess zu unterstützen. Trotz dessen sollte der Einsatz immer kritisch reflektiert werden und auch das pädagogische Handeln entsprechend angepasst werden. Lehrpersonen kommen hierbei eine sehr zentrale Rolle zu, da diese die ausführende Kraft bezüglich dem Einsatz digitalen Werkzeuge im Unterricht ist
und diese in ihre Unterrichtsgestaltung und -durchführung sinnvoll einbauen soll.
Literatur
Kultusministerium: Gymnasium - Mathematik. Bildungspläne Baden-Württemberg. Online verfügbar unter https://www.bildungsplaene-bw.de/,Lde/LS/BP2016BW/ALLG/GYM/M, zuletzt geprüft am 24.10.2022.
primakom - Deutsches Zentrum für Lehrkräftebildung Mathematik: Modellieren. Online verfügbar unter https://primakom.dzlm.de/node/236, zuletzt geprüft am 26.10.2022.
Pallack, A. (2018): Digitale Medien im Mathematikunterricht der Sekundarstufen I + II. Berlin, Heidelberg: Springer Spektrum (Mathematik Primarstufe und Sekundarstufe I + II). Online verfügbar unter http://www.springer.com/.
Pallack, A. (2020): Lernvideo zum MK-Modell. Online verfügbar unter https://pallack.de/lernvideo- zum-mk- modell, zuletzt geprüft am 01.11.2022.
Thurm, D.: Digitale Werkzeuge im Mathematikunterricht integrieren. Dissertation. Springer
Fachmedien Wiesbaden.
Abb.1: lizenzfreie Abbildungen der Plattform https://pixabay.com/
Abb.2: Modellierungskreislauf: Borromeo Ferri, Rita; Greefrath, Gilbert; Kaiser, Gabriele (Hg.) (2013):
Mathematisches Modellieren für Schule und Hochschule. Theoretische und didaktische Hintergründe. Wiesbaden: Springer Sprektrum (Realitätsbezüge im Mathematikunterricht), S. 18.