Aynı Alan Farklı Kenar uzunlukları
 aracı yardımıyla ilk olarak başlangıç noktası "1" ve bitişi "100" ve artışı "1" olan bir sürgü (d_1 sürgüsü) oluşturunuz. Bu sürgüdeki amaç girdi alanına yazılacak sayının (alan belirtecek) bu sürgü ile yapılandırılmasıdır (Bu sürgü saklanır)
aracı yardımıyla ilk olarak başlangıç noktası "1" ve bitişi "100" ve artışı "1" olan bir sürgü (d_1 sürgüsü) oluşturunuz. Bu sürgüdeki amaç girdi alanına yazılacak sayının (alan belirtecek) bu sürgü ile yapılandırılmasıdır (Bu sürgü saklanır)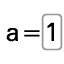 girdi alanı aracı yardımıyla "Alan"
girdi alanı aracı yardımıyla "Alan"  isminde girdi alanı oluşturulur ve bağlı nesne olarak "d_1" seçilir.
isminde girdi alanı oluşturulur ve bağlı nesne olarak "d_1" seçilir.
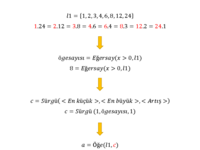
 aracı yardımıyla l1=BölenlerListesi(Sayı)=BölenlerListesi(d_1) komutu ile bölenler listesi oluşturulur.
aracı yardımıyla l1=BölenlerListesi(Sayı)=BölenlerListesi(d_1) komutu ile bölenler listesi oluşturulur.- ögesayısı=EğerSay( <Şart>,liste)=EğerSay(x > 0, l1) komutu kullanılarak bölen sayısı=ögesayısı tespit ettirilir.
 aracı yardımıyla başlangıç noktası "1" ve bitişi "ögesayısı" ve artışı "1" olan bir sürgü (c sürgüsü) oluşturunuz. Bu sürgüdeki amaç ise dikdörtgenin alan değerinin çarpanlarının birbiri ile çarpılması için farklı durumları oluşturmaktır. Bu doğrultuda örneğin 24 sayısının 1,2,3,4,6,8,12 ve 24 olmak üzere 8 tane çarpanı("ögesayısı") vardır. Bunların 1.24=2.12=3.8=4.6=6.4=8.3=12.2=24.1 olmak üzere 8 farklı durumu bu sürgü ile gösterilecektir.
aracı yardımıyla başlangıç noktası "1" ve bitişi "ögesayısı" ve artışı "1" olan bir sürgü (c sürgüsü) oluşturunuz. Bu sürgüdeki amaç ise dikdörtgenin alan değerinin çarpanlarının birbiri ile çarpılması için farklı durumları oluşturmaktır. Bu doğrultuda örneğin 24 sayısının 1,2,3,4,6,8,12 ve 24 olmak üzere 8 tane çarpanı("ögesayısı") vardır. Bunların 1.24=2.12=3.8=4.6=6.4=8.3=12.2=24.1 olmak üzere 8 farklı durumu bu sürgü ile gösterilecektir.- Herhangi bir kenar uzunluğunu belirlemek için listeden bir eleman belirlenir. Bunun için a=Öge(liste,sayı)=Öge(l1,c) komutu kullanılır. Böylelikle çarpanlardan bir elemanı sırasıyla sürgü yardımıyla seçiyorsunuz. Örneğin c=5 olduğunda l1={1,2,3,4,6,8,12,24} ise Öge(l1,5)=6 olacaktır
 aracı yardımıyla başlangıç noktası A=(0,0) işaretlenir.
aracı yardımıyla başlangıç noktası A=(0,0) işaretlenir.- Dikdörtgenin uzun kenarı olan B noktasını B=(x(A)+a,0) Bu durumda dikdörtgenin yatay kenar uzunluğu B=(0+6,0)=(6,0) olacaktır.
- e=ögesayısı - c + 1 ile örneğin 8 öge var ve sürgü 1 konumunda iken 8-1+1=8 yani 1 ile 24 eşleşmiş olacaktır. Ya da sürgü 2 konumunda iken 8-2+1=7 yani 2 ile 12 eşleşmiş olacaktır.
- b=Öge(l1,e) komutu ile e. sıradaki öge b ile belirlenmiş olacaktır. Örneğin c=5 olduğunda e=4 olduğunda b=4 olacaktır. Buradaki amaç "a" ile seçtiğimiz ikinci çarpana eş bulmak olacaktır.
- Burada a ve b dikdörtgenin diğer kenarlarını belirlemek için kullanacağımız sayılar. Hatırlarsanız A=(0,0), B=(x(A)+a,0) idi şimdi de C=(0,y(A)+b) ve D=(x(A)+a,y(a)+b) olacaktır.
 sekmesi yardımıyla A, B, C ve D noktaları birleştirilerek ABCD dikdörtgeni elde edilir.
sekmesi yardımıyla A, B, C ve D noktaları birleştirilerek ABCD dikdörtgeni elde edilir.
 yardımıyla farklı dörtgenler oluşturulur.
yardımıyla farklı dörtgenler oluşturulur.
 aracı yardımıyla ilk olarak başlangıç noktası "1" ve bitişi "100" ve artışı "1" olan bir sürgü (d_1 sürgüsü) oluşturunuz. Bu sürgüdeki amaç girdi alanına yazılacak sayının (alan belirtecek) bu sürgü ile yapılandırılmasıdır (Bu sürgü saklanır)
aracı yardımıyla ilk olarak başlangıç noktası "1" ve bitişi "100" ve artışı "1" olan bir sürgü (d_1 sürgüsü) oluşturunuz. Bu sürgüdeki amaç girdi alanına yazılacak sayının (alan belirtecek) bu sürgü ile yapılandırılmasıdır (Bu sürgü saklanır)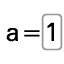 girdi alanı aracı yardımıyla "Alan"
girdi alanı aracı yardımıyla "Alan"  isminde girdi alanı oluşturulur ve bağlı nesne olarak "d_1" seçilir.
isminde girdi alanı oluşturulur ve bağlı nesne olarak "d_1" seçilir.
 aracı yardımıyla l1=BölenlerListesi(Sayı)=BölenlerListesi(d_1) komutu ile bölenler listesi oluşturulur.
aracı yardımıyla l1=BölenlerListesi(Sayı)=BölenlerListesi(d_1) komutu ile bölenler listesi oluşturulur. aracı yardımıyla başlangıç noktası "1" ve bitişi "ögesayısı" ve artışı "1" olan bir sürgü (c sürgüsü) oluşturunuz. Bu sürgüdeki amaç ise dikdörtgenin alan değerinin çarpanlarının birbiri ile çarpılması için farklı durumları oluşturmaktır. Bu doğrultuda örneğin 24 sayısının 1,2,3,4,6,8,12 ve 24 olmak üzere 8 tane çarpanı("ögesayısı") vardır. Bunların 1.24=2.12=3.8=4.6=6.4=8.3=12.2=24.1 olmak üzere 8 farklı durumu bu sürgü ile gösterilecektir.
aracı yardımıyla başlangıç noktası "1" ve bitişi "ögesayısı" ve artışı "1" olan bir sürgü (c sürgüsü) oluşturunuz. Bu sürgüdeki amaç ise dikdörtgenin alan değerinin çarpanlarının birbiri ile çarpılması için farklı durumları oluşturmaktır. Bu doğrultuda örneğin 24 sayısının 1,2,3,4,6,8,12 ve 24 olmak üzere 8 tane çarpanı("ögesayısı") vardır. Bunların 1.24=2.12=3.8=4.6=6.4=8.3=12.2=24.1 olmak üzere 8 farklı durumu bu sürgü ile gösterilecektir. aracı yardımıyla başlangıç noktası A=(0,0) işaretlenir.
aracı yardımıyla başlangıç noktası A=(0,0) işaretlenir. sekmesi yardımıyla A, B, C ve D noktaları birleştirilerek ABCD dikdörtgeni elde edilir.
sekmesi yardımıyla A, B, C ve D noktaları birleştirilerek ABCD dikdörtgeni elde edilir.
 yardımıyla farklı dörtgenler oluşturulur.
yardımıyla farklı dörtgenler oluşturulur.