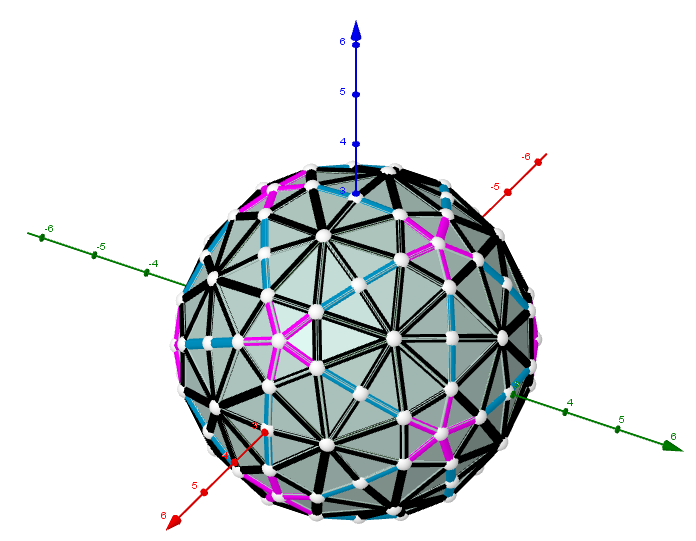
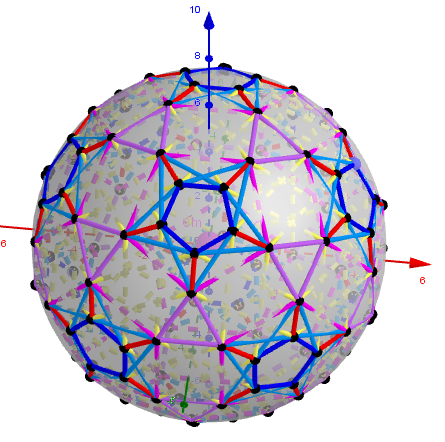
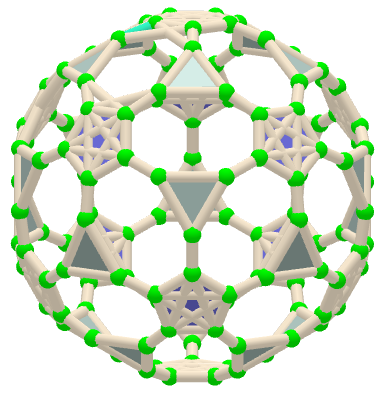
Images 1. Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
A polyhedron is constructed whose V=120 vertices are the points of the trisection of the segments the same length 1st order(g=1) of the Biscribed Pentakis Dodecahedron.
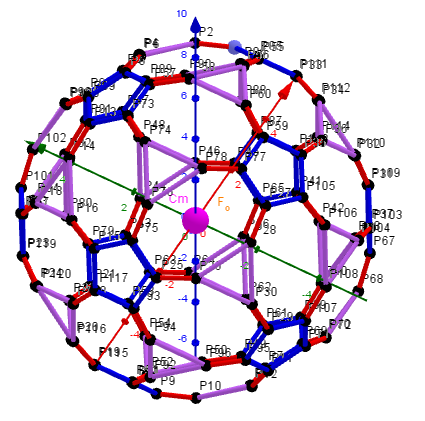
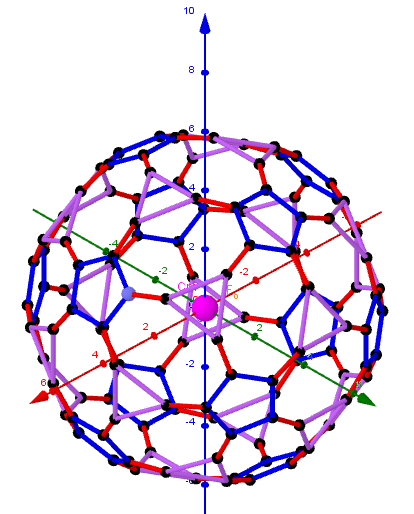
Geometric Constructions are in Applet: Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron.
Generating Elements of mesh modeling the surfaces of convex polyhedrons and its dual images and Coloring edges and faces of polyhedra is in Applet.
*The Seven Zonish Rhombicosidodecahedra

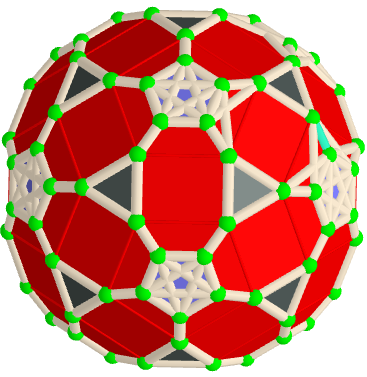
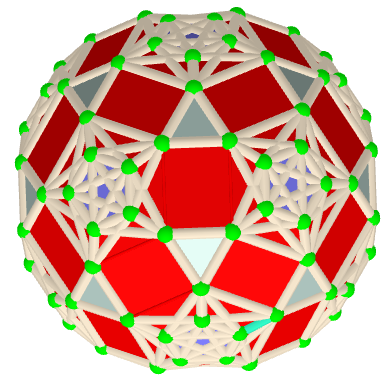
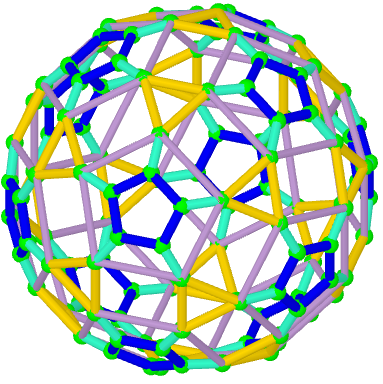
n=120; Rhombicosidodecahedron
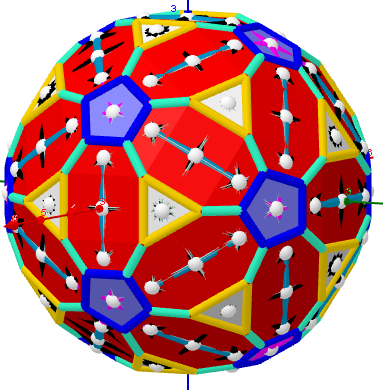
![If we assume that all quadrilaterals lie in the same plane, then our polyhedron approximately looks like
ht[url=https://robertlovespi.net/2014/06/02/zonish-versions-of-the-rhombicosidodecahedron/]tps://robertlovespi.net/2014/06/02/zonish-versions-of-the-rhombicosidodecahedron/[/url]
[b]Vertices:[/b] V =120.
[b]Faces [/b]F =62. 20{3}+(30){8}+12{5}
[b]Edges:[/b] E =180. 60+60+60- The order of the number of edges in this polyhedron according to their length.](https://www.geogebra.org/resource/wnt9hrfu/wkTef2l5AbcTOaou/material-wnt9hrfu.png)
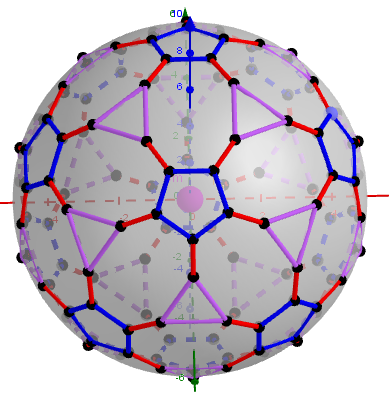
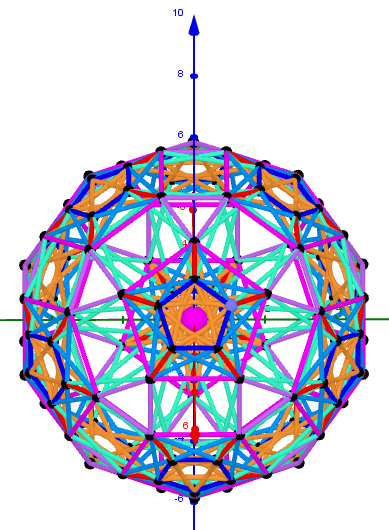
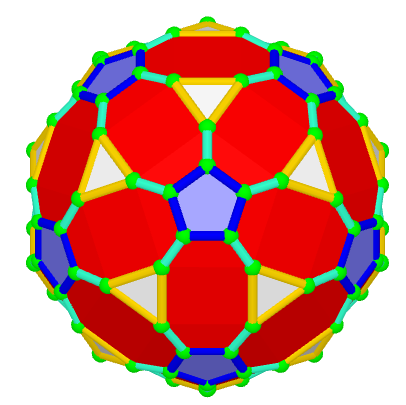
Dual