Geometrische Grundlagen

저자:J.M.

Hier findest du viele Begriffe, die dir durch den Unterricht schon bekannt sein sollten (zumindest in den höheren Klassen). Aber nimm dir ruhig mal Zeit und schau sie dir an, diese Begriffe sind Grundlagen für gute Mathematik.

Flächen

Flächen in der Mathematik befinden sich im zweidimensionalen Raum. Sie haben daher zwei senkrecht aufeinander stehende Längen, wie beim Koordinatensystem. Die Flächen können durch Seiten begrenzt werden, dadurch entstehen Figuren. Was auf den ersten Blick für dich jetzt vielleicht komisch klingt, erklärt sich am besten durch das folgende Bild:

Grundfläche

Die Grundfläche nennt man die Fläche, auf der ein Körper steht (oder die wir zur Berechnung als solche betrachten!) Beispiele von Grundflächen in der Geometrie • Die Grundfläche eines Quaders ist ein Rechteck. • Die Grundfläche einer Pyramide ist ein Vieleck. • Die Grundfläche eines Zylinders ist ein Kreis oder eine Ellipse. • Die Grundfläche eines Kegels ist ein Kreis.

Seitenfläche

Seitenfläche: Damit ist der Rand von Körpern gemeint (also die Begrenzung).

Deckfläche

Die Deckfläche nennt man die Fläche, die einen Körper nach oben abdeckt (quasi der Deckel).

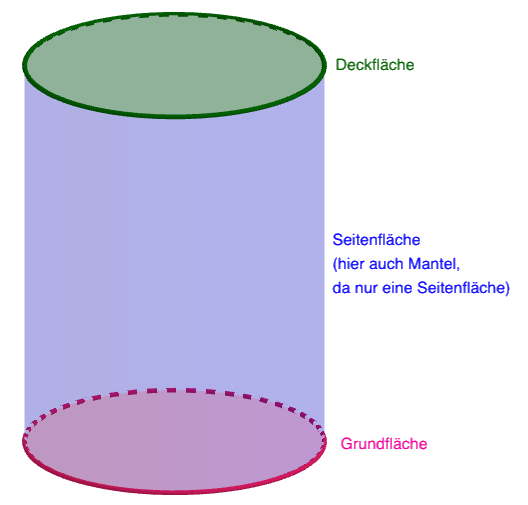
Grund-, Seiten- und Deckfläche am Beispiel des Zylinders

Flächeninhalt

Der Flächeninhalt einer Figur beschreibt das, was innerhalb der Figur ist. Er ist als Fläche zweidimensional und wird daher in der Einheit immer mit "hoch 2" angegeben (Bsp.:

) Du findest hier die Flächeninhalte folgender Figuren: - Dreieck allgemein bzw. Dreieck Trigonometrie - Quadrat - Rechteck - Raute - Parallelogramm - Drachen - Gleichschenkliges Trapez - Trapez - Kreis - Kreisring - Kreisausschnitt - Kreisabschnitt - Sechseck - Regelmäßiges Vieleck (n-Eck)

Umfang

Der Umfang gibt an, wie lang die Seiten einer Figur insgesamt sind. Man zählt sie also einfach zusammen. Bei den Vielecken gilt: der Name der Figur verrät dir, wie viele Seiten du zusammenzählen musst. Beispiel: Dreieck -> drei Seiten Achteck -> acht Seiten Beim Kreis als eckenlose Figur entspricht der Umfang der Länge seiner Kreislinie.

Diagonale

Unter einer Diagonale versteht man in der Mathematik eine Gerade, die in geometrischen Flächen oder Körpern von einer Ecke zu einer anderen Ecke verläuft. Dabei geht diese Gerade immer durch die Fläche oder den Körper. In den folgenden Beispielen siehst du rot eingezeichnet die Diagonalen:

[size=85]Eine Diagonale im Fünfeck[/size] — Eine Diagonale im Fünfeck

Eine Diagonale im Quader

Koordinatensystem

Ein Koordinatensystem besteht aus zwei senkrecht zueinander stehenden Zahlenstrahlen. Dadurch kann man Zuordnungen grafisch darstellen. Es dient der Visualisierung.

[size=85]Die Quadranten werden gegen den Uhrzeigersinn benannt. Warum? Weil auf diesem Weg immer nur ein Vorzeichen der x- und y-Werte gewechselt wird und mit dem x-Wert begonnen wird:

[table][tr][td]Quadrant[/td][td]Vorzeichen x-Wert[/td][td]Vorzeichen y-Wert[/td][/tr][tr][td]1[/td][td]+[/td][td]+[/td][/tr][tr][td]2[/td][td]-[/td][td]+[/td][/tr][tr][td]3[/td][td]-[/td][td]-[/td][/tr][tr][td]4[/td][td]+[/td][td]-[/td][/tr][/table][/size] — Die Quadranten werden gegen den Uhrzeigersinn benannt. Warum? Weil auf diesem Weg immer nur ein Vorzeichen der x- und y-Werte gewechselt wird und mit dem x-Wert begonnen wird:
Quadrant Vorzeichen x-Wert Vorzeichen y-Wert
1 + +
2 - +
3 - -
4 + -

Körper

Ein Körper ist eine dreidimensionale Figur. Er besitzt Grenzseiten, die sogenannten Flächen. Die Körper werden in drei Kategorien eingeteilt: 1. Polyeder (Körper aus Vielecken) 2. Konvexe Körper (regelmäßige Körper) 3. Rotationskörper (Kreisrotationskörper) Hier ein paar Beispiele: Kugel, Pyramide, Würfel, Kreiszylinder, Kegel

Polyeder

Wörtlich übersetzt bedeutet Polyeder Vielflächner. Du hast hier also alle Körper, die durch gerade Flächen begrenzt sind, also durch Dreiecke, Vierecke oder weitere Vielecke. Beispiele für Polyeder: Würfel, Quader, Prisma, Pyramide, Regelmäßige Körper Obacht: Sobald ein Kreis als Fläche dabei ist, spricht man von einem Rotationskörper.

Rotationskörper

Rotationskörper entstehen durch Rotation einer Fläche um eine Achse. In diesem Beispiel entsteht ein Zylinder durch Rotation eines Rechtecks.

Mantel

Ein Körper hat mehrere Flächen. Jeder Körper hat eine Grundfläche, manche auch eine Deckfläche. Die sogenannte Mantelfläche beinhaltet alle Flächen des Körpers ohne Grundfläche und Deckfläche. Er ist die Summe der Seitenflächen.

Oberflächeninhalt

Der Oberflächeninhalt ist die Summe aller nach außen abgrenzenden Flächen eines Körpers. Wir berechnen den Oberflächeninhalt für folgende Körper: - Würfel - Quader - Prisma - quadratische Pyramide - regelmäßige Dreieckspyramide (Tetraeder) - regelmäßige Sechseckspyramide - regelmäßige n-Ecks-Pyramide - Zylinder - Kegel - Kugel - Oktaeder - Dodekaeder - Ikosaeder

Volumen

Das Volumen beschreibt den Rauminhalt eines Körpers. Wir berechnen das Volumen für folgende Körper: - Würfel - Quader - Prisma - quadratische Pyramide - regelmäßige Dreieckspyramide (Tetraeder) - regelmäßige Sechseckspyramide - regelmäßige n-Ecks-Pyramide - Zylinder - Kegel - Kugel - Oktaeder - Dodekaeder - Ikosaeder

Längen

Überall im Alltag triffst du auf Längen. Deinen Schulweg, deine Köprergröße, jeder Gegenstand hat mindestens eine Länge. Diese sind messbar, z.B. in Metern (das ist auch die Grundeinheit der Länge) In der Mathematik misst man die Länge immer entlang einer Geraden, wie beim Zahlenstrahl.

Maßstab

Parallele

Wenn zwei Geraden zueinander immer den gleichen Abstand (rechtwinklig) haben, dann sagt man: sie verlaufen parallel. In diesem Beispiel haben die Geraden g und h immer denselben Abstand: sie sind parallel (g ∥ h). Auch die Geraden i und j haben immer denselben Abstand: auch sie sind parallel (i ∥ j)

Seite

Der Begriff Seite ist in der Mathematik immer etwas schwammig. Wenn du den Begriff hörst, dann merke dir bitte folgendes: damit ist die Begrenzung einer zweidimensionalen Figur gemeint, quasi deren Rand. Der Begriff kann auch in einem Wort enthalten sein: Seitenfläche: Damit ist der Rand von Körpern gemeint (also die Begrenzung)

Strecke, Halbgerade, Gerade

Eine Strecke ist die kürzeste Verbindung zwischen zwei Punkten (Startpunkt und Endpunkt). Eine Halbgerade startet wie die Strecke im Startpunkt, hört aber nicht im Endpunkt auf, sondern läuft in gleicher Richtung unendlich weiter. Eine Gerade kommt aus der Unendlichkeit, läuft durch Start- und Endpunkt und weiter bis in die Unendlichkeit