5-3: Centroid & Orthocenter of a Triangle (with Euler Line)

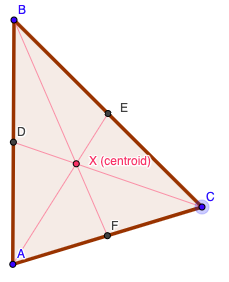
Locate the Centroid of a Triangle:
Locate the Orthocenter of a Triangle:
Part 2: Large Triangles (You may work on this with a classmate)
- Ask your teacher for a large whiteboard triangle
- Draw the three MEDIANS for the triangle (connect each vertex to the midpoint of the opposite side)
- Label the CENTROID of the triangle
- Try to balance the triangle at the centroid
Centroid Theorem: (using the LARGE TRIANGLE)
| 
|
Attach your picture below.
>>> Record your conjecture on your handout paper.
Part 3: Euler Line
Use the applet below to answer the questions in this section.
Task 4
- Show only the Perpendicular Bisectors of sides (circumcenter)
- Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
The location of the circumcenter is _____ an acute triangle, _____ a right triangle, and _____ an obtuse triangle. [choices: inside, outside, on]
>>> Record your conjecture on your handout paper.Task 5
- Show only the Lines Containing Altitudes (orthocenter)
- Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Task 6
- Show only the Angle Bisectors (incenter)
- Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Task 7
- Show only the Medians (centroid)
- Drag a vertex to experiment with different types of triangles (scalene, isosceles, acute, right, obtuse, equiangular/equilateral)
Task 8
- Leave the centroid marked and show the centroid measurements.
- Test your hypothesis from Part 2: Large Triangles.
Task 9
The Euler Line is named after an 18th century mathematician Leonhard Euler (pronounced 'oiler')
Which of the four special points [orthocenter, circumcenter, incenter, centroid] are always on the Euler Line. (these points are collinear)
>>> Record your conjecture on your handout paper.
Task 10
When is it possible for all four special points to be collinear?
>>> Record your conjecture on your handout paper.
Task 11
When is it possible for all four special points to be concurrent?
>>> Record your conjecture on your handout paper.