1. Concepto de plano como lugar geométrico y sus ecuaciones.
¿Cómo se define un plano?
Plano
- Si una recta tiene más de un punto en un plano, entonces la recta está contenida en el plano.
- Tres puntos no alineados generan un único plano.
- Si dos planos distintos se cortan, su intersección es una recta.
- Dos planos que no tienen ningún punto en común se denominan paralelos.
Sabiendo esto, y a manera de resumen, un plano en el espacio queda completamente determinado dando tres de sus puntos que no sean colineales (es decir, que no estén sobre una misma línea recta) o también dando uno de sus puntos y un vector geométrico no nulo perpendicular al plano. Se entiende que un vector del espacio es perpendicular a un plano si es perpendicular a todo vector con y en .
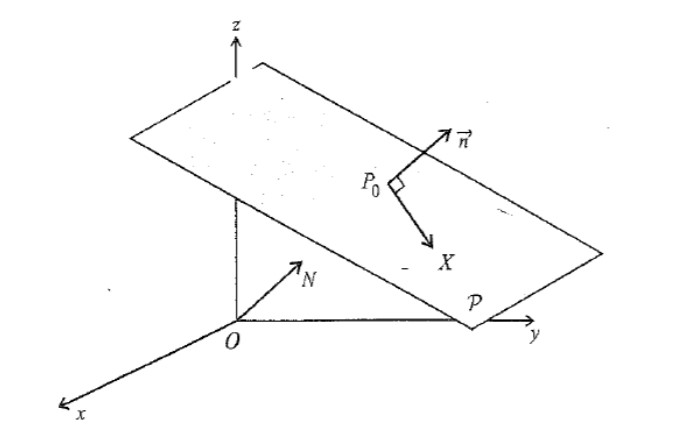
Todo vector geométrico no nulo y perpendicular al plano se dirá un vector normal a dicho plano. Considerando un plano y siendo un punto de y un vector normal a , podemos emplear el producto escalar para obtener una ecuación del plano que sea completamente análoga a la ecuación en forma normal de una recta en el plano. En efecto un punto del espacio está en el plano si y sólo si el vector es perpendicular a , es decir, si y sólo si:
Ahora, si , esta ecuación se puede expresar, usando únicamente vectores algebraicos, en la forma:
...(1)
En adelante, concluimos en decir que un vector de es un vector normal a un plano π siempre que el vector geométrico sea un vector normal a . La ecuación (1) es una ecuación vectorial no paramétrica para la cual es llamada una ecuación en forma normal. Ahora bien, si , y , al sustituir , y en la ecuación (1) y realizar el producto escalar, dicha ecuación se transforma en la ecuación escalar
...(2)
la cual es por tanto una ecuación para el plano ; si realizamos los productos indicados en (2), esta ecuación se puede escribir como:
Donde Podemos afirmar entonces que todo plano en el espacio tiene una ecuación de la forma:
...(3)
La cual llamaremos ecuación en forma general, donde y son constantes y o o