Binomio de Newton
El Teorema del Binomio de Newton fue descubierto en 1665, su importancia es que a partir de este hallazgo Newton y los matemáticos de la época intuyeron que era posible operar con series infinitas de la misma manera que con expresiones polinómicas finitas siendo este principio de un sin número series infinitas que aparecerían más adelante.
TRIANGULO DE PASCAL

![[size=150]
DESARROLLO DEL BINOMIO[/size]
[math]\binom{n}{k}=\frac{n!}{k!\left(n-k\right)!}[/math]
[math]\left(x+y\right)^n=\sum^n_{k=0}\binom{n}{k}x^{n-k}y^k[/math]
[math]\left(x+y\right)^n=\binom{n}{0}x^{n-0}y^0+\binom{n}{1}x^{n-1}y^1+\binom{n}{2}x^{n-2}y^2....+\binom{n}{n}x^{n-n}y^n[/math]
[math]\left(x+y\right)^n=x^n+nx^{n-1}y+\frac{n\left(n-1\right)}{2}x^{n-2}y^2+...+y^n[/math]](https://www.geogebra.org/resource/ek64nhwm/atgY4hScUGBFqKzv/material-ek64nhwm.png)
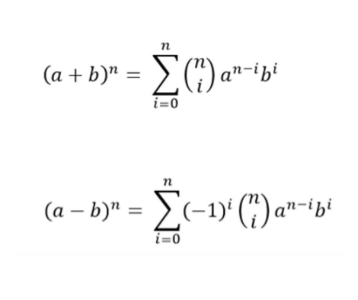
CÁLCULO DEL TÉRMINO K-ÉSIMO
El número de términos será igual a (n+1)
Primer Término k=0
Segundo Término k=1
EJEMPLOS
Hallar el 4to término de :
Desarrollo:
Para el 4to término k=3
Hallar el 3er término de :
Desarrollo:
Para el 3er término k=2