5. Angulo entre dos rectas
El ángulo que se forma entre dos rectas en R3 cuando se cruzan (Aún si no se intersecan en un punto) se puede calcular a través del ángulo que forman sus vectores de dirección.
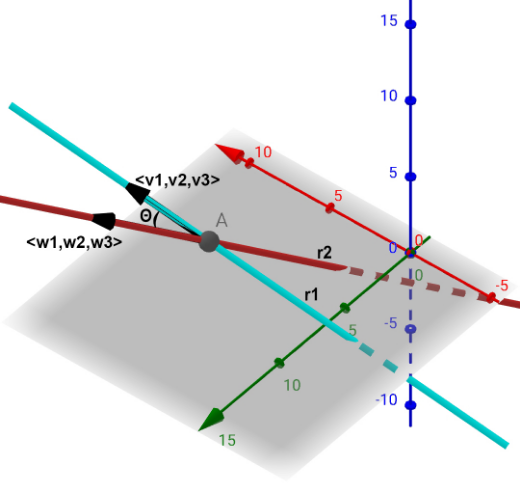
Asi, sean dos rectas:
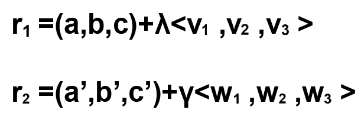
Con sus vectores de dirección n=<v1,v2,v3> y m=<w1,w2,w3>
El ángulo entre r1 y r2 se calcula como:
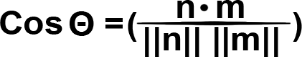
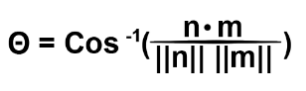
Nótese como para que dos rectas sean perpendiculares entre sí, el producto escalar de sus vectores de dirección debe ser 0.
Ejemplo Interactivo
Ejercicio.
Determine el ángulo que hay entre las rectas r1 : r2: .