Typische Graphen von reellen Polynomfunktion
Ausgehend von einfachen Beispielen sollen allgemeine Aussagen über die Anzahl der Nullstellen, Extremstellen und Wendestellen von Polynomfunktionen aufgestellt werden.
Zur Erinnerung ein Polynom vom Grad n kann im Allgemeinen wie folgt angeschrieben werden:
Die reellen Zahlen nennt man Koeffizienten und die höchste Potenz n entspricht dem Grad des Polynoms.
_______________________________________________________________________________
Die wichtigsten Polynomfunktionen:
n=0:
konstante Funktion
- 0 oder bei unendlich viele Nullstellen
- 0 Extremstellen
- 0 Wendestellen
- Graph verläuft parallel zur x-Achse
Graph einer allgemeinen konstanten Funktion:

Graph einer konstanten Funktion f(x)=0:
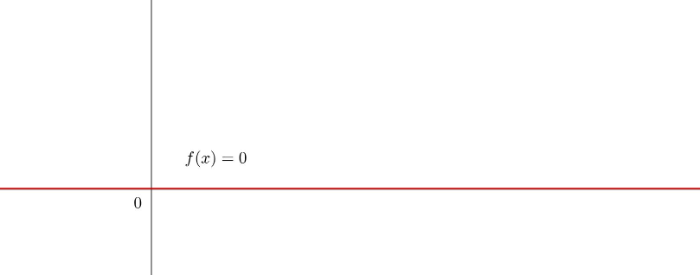
_______________________________________________________________________________
n=1:
lineare Funktion
- genau 1 Nullstelle
- 0 Extremstellen
- 0 Wendestellen
- Graph schneidet die x-Achse an genau einer Stelle
Typischer Graph einer linearen Funktion:
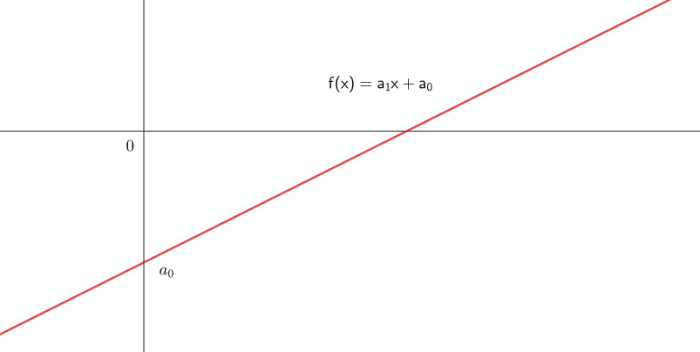
_______________________________________________________________________________
n=2:
quadratische Funktion
- 0,1 oder 2 Nullstellen (Stichwort: Diskriminante)
- 1 Extremstellen bei
- 0 Wendestellen
- Graph ist eine Parabel
Typische Graph einer quadratischen Funktion:
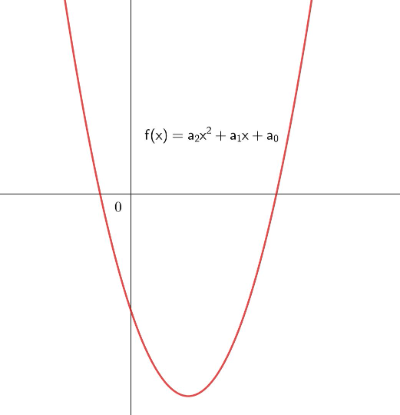
_______________________________________________________________________________
n=3:
kubische Funktion
- 1,2 oder 3 Nullstellen
- 0 ode 2 Extremstellen
- 1 Wendestellen
- Typischer Graph ist s-förmig
Typischer Graph eines Polynoms dritten Grades:
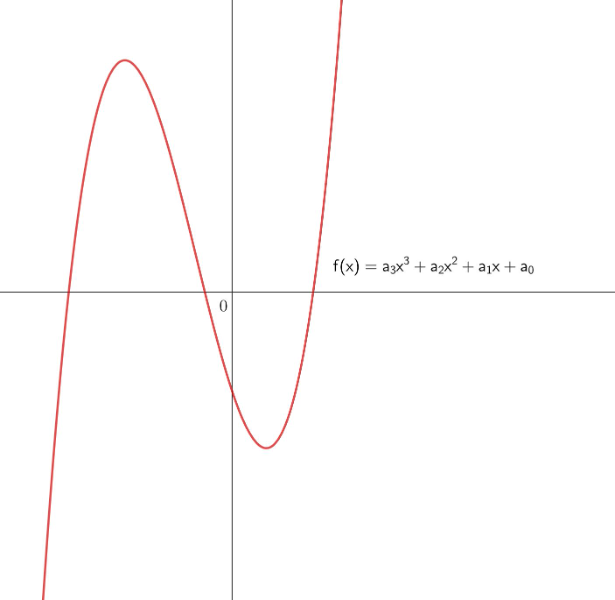
Nicht s-förmiger Graph eines Polynoms dritten Grades:
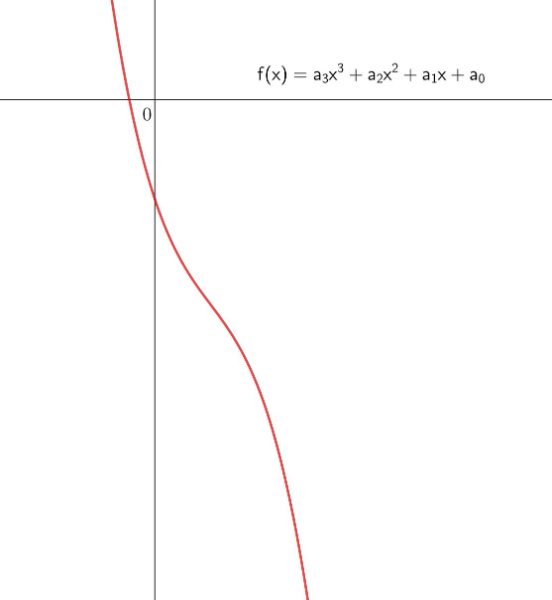
_______________________________________________________________________________
n=4:
- 0,1, ..., 4 Nullstellen
- 1 ode 3 Extremstellen
- 0 oder 2 Wendestellen
- Typischer Graph ist w-förmig
Typischer Graph eines Polynoms vierten Grades:
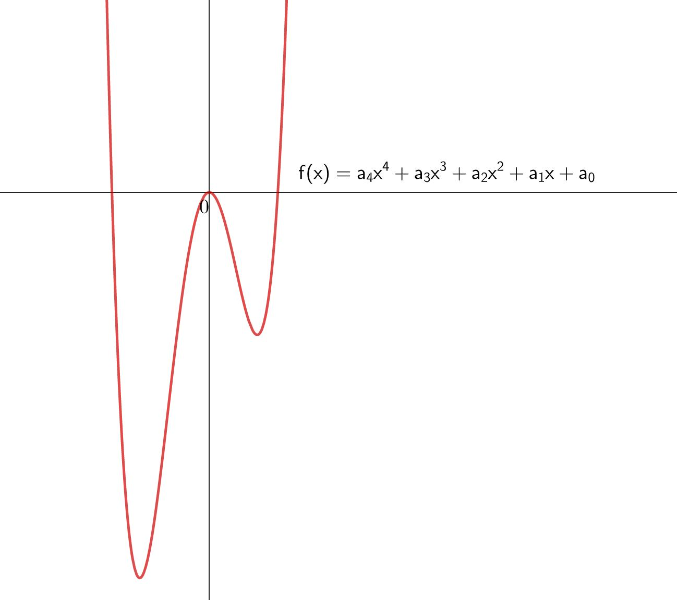
Nicht w-förmiger Graph eines Polynoms vierten Grades:
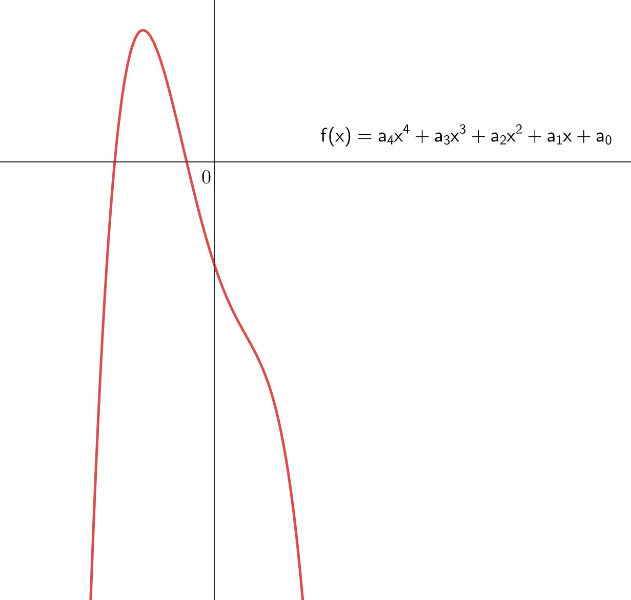
_______________________________________________________________________________
_______________________________________________________________________________
Allgemeine Aussagen:
Nullstellen:
(Wenn n ungerade ist dann existiert mindestens eine reelle Nullstelle!)
Extremstellen:
Wendestellen:
_______________________________________________________________________________
_______________________________________________________________________________
Aufgaben:
Die abgebildeten Graphen gehören zu Polynomfunktionen vom Grad 2, 3 oder 4. Gib den kleinstmöglichen Grad an!
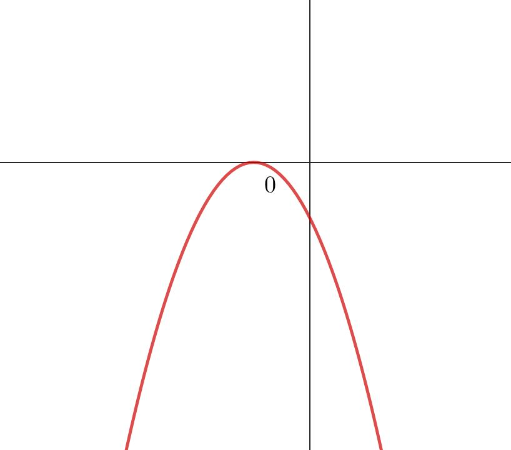
Gib den kleinstmöglichen Grad an!
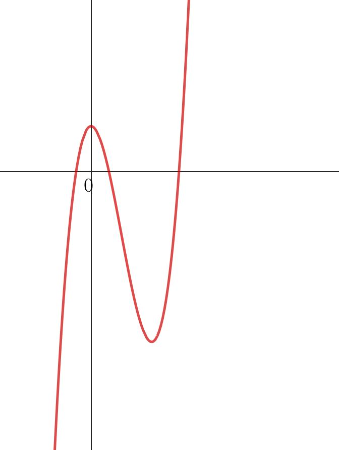
Gib den kleinstmöglichen Grad an!
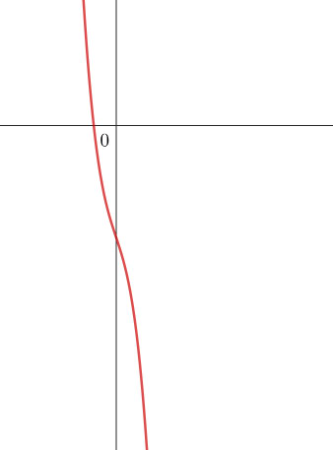
Gib den kleinstmöglichen Grad an!
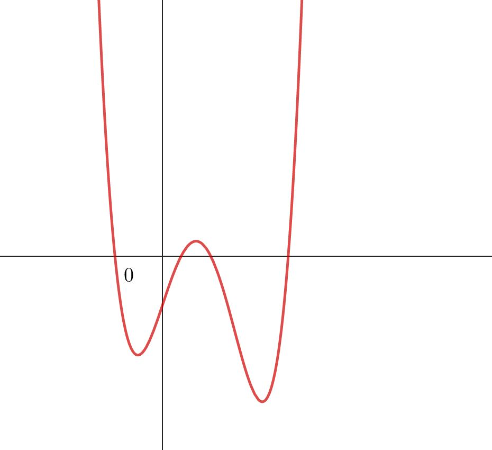
Gib den kleinstmöglichen Grad an!
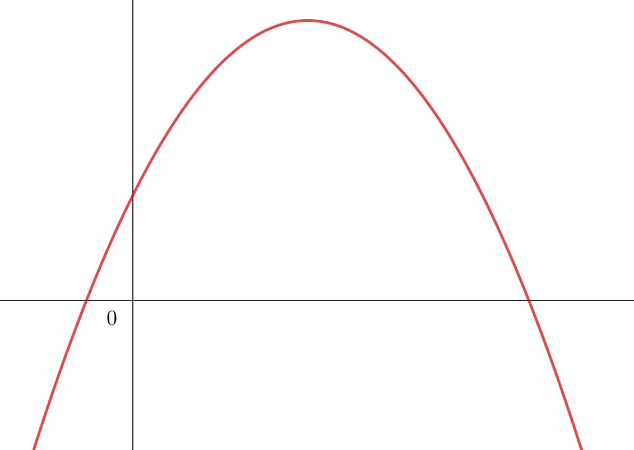
Gib den kleinstmöglichen Grad an!
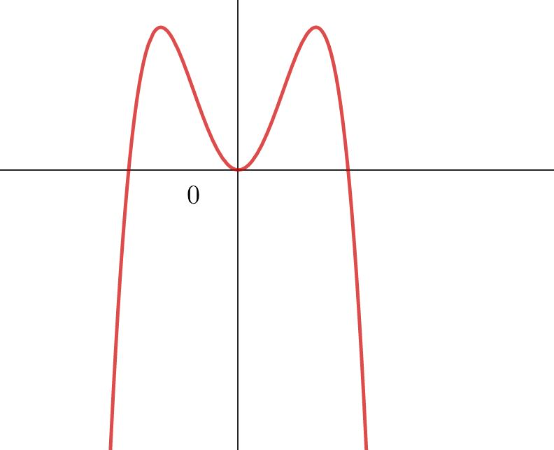
Gib den kleinstmöglichen Grad an!
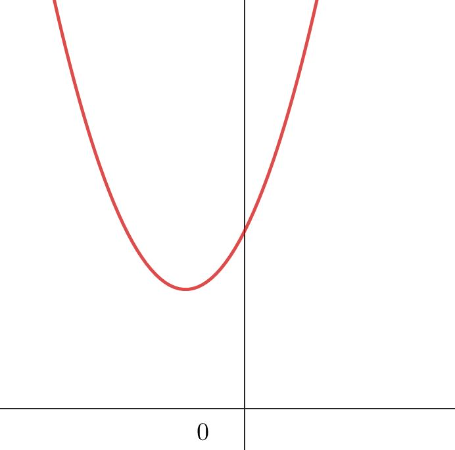
Gib den kleinstmöglichen Grad an!
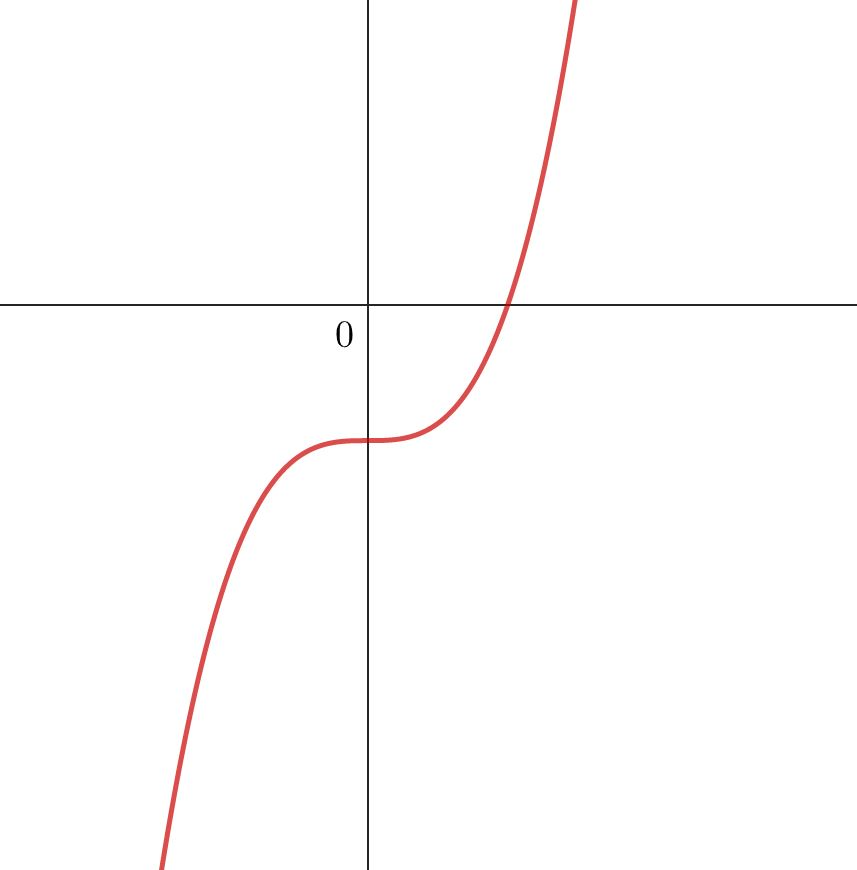
Gib den kleinstmöglichen Grad an!
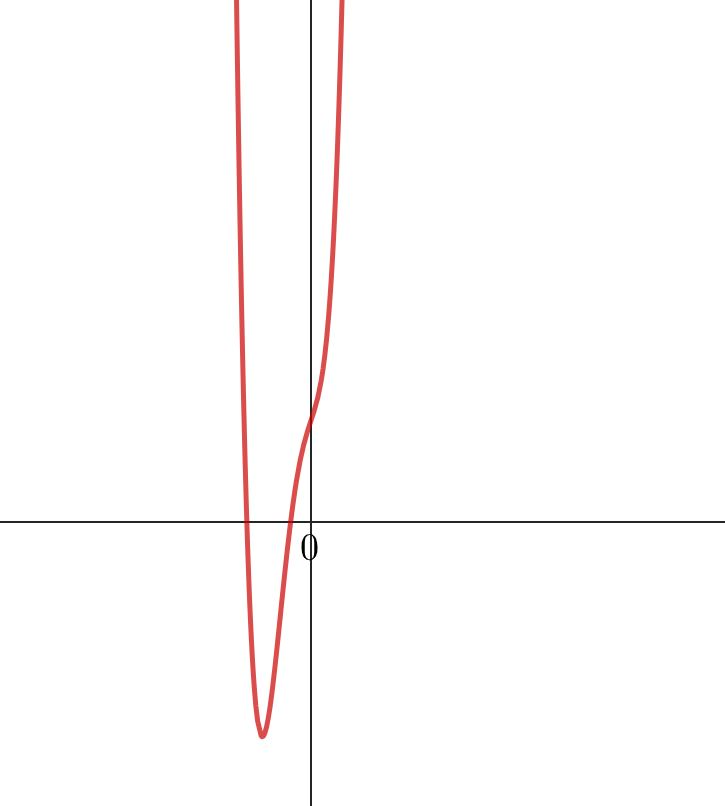
Gib den kleinstmöglichen Grad an!
Nullstellensatz von Bolzano
Für jedes reelle Polynom f mit einem ungeraden Grad lassen sich zwei Zahlen finden sodass gilt. Schlussfolgere was das für die Existenz einer reellen Nullstelle bedeutet!