Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

RAZONES Y PROPORCIONES

Autor:JOS GABRIEL ECHEVERR A VILLAG MEZ

Proporcionalidad

RAZONES Y PROPORCIONES Las razones y proporciones nacen de la necesidad de dar solución a ciertos problemas de reparto, como el cobro de impuestos, el cambio de moneda, la geometría relacionada con la medición y semejanza de figuras. RAZONES
  • La razón es una comparación entre dos o más cantidades, puede expresarse mediante una fracción. Si las cantidades a comparar son a y b la razón entre ellas se escribe como el cociente entre dos cantidades a/b con b diferente de cero.
  • La razón se puede expresar como a/b o a:b y en ambos casos se lee: "a es a b"
  • En una razón a/b, a es el antecedente y b es el consecuente.
EJEMPLO:  En un colegio hay 300 niñas y 200 niños. a- Determine la razón entre la cantidad de niñas y la cantidad de estudiantes del colegio. R/: La cantidad de estudiantes es de 500 y la cantidad de niñas es de 300, por lo tanto la razón es de 300 / 500 o sea 3/5, lo que quiere decir es que por cada 5 estudiantes que hay en el colegio 3 son niñas. b- Determine la razón entre la cantidad de niños y la cantidad de estudiantes del colegio. R/: La cantidad de estudiantes es de 500 y la cantidad de niños es de 200, por lo tanto la razón es de 200 / 500 o sea 2/5, lo que quiere decir es que por cada 5 estudiantes que hay en el colegio 2 son niños. EJEMPLO:  Si un Trapecio isósceles se compara su altura que mide 4 cm, con su base que mide 6 cm se tiene la razón. PROPORCIONES
  • Es la igualdad de dos razones de una misma clase que tenga el mismo valor de la razón.
  • La proporción entre las razones a/b y c/d con b y d diferentes de cero, se escribe:
a/b = c/d o a : b :: c : d y se lee "a es a b como c es a d". EJEMPLO: Las razones 7/3 y 21/9  forman una proporción ya que al simplificar 21 / 9 se obtiene la fracción 7/3, en cambio las razones 1/2 y 2/3 no forman una proporción ya que ninguno de los dos se puede obtener a partir de la complificación o la simplificación de la otra.
  • En la proporción a/b = c/d, a y d son los extremos y b y c son los medios.
  • Cuando en una proporción, los medios o los extremos son iguales, la proporción recibe el nombre de proporción continua. por ejemplo 3/9 = 9/27; 9 es la media proporcional de los términos 3 y 27.

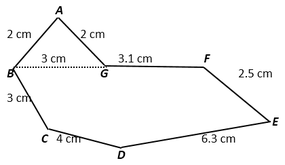
Ejercicio de práctica:

a- La razón entre el perímetro de la figura y la medida del lado FG. b- La razón entre la medida del lado CD y el lado EF. c- La razón entre el perímetro y la suma de las longitudes AB y DE. d- La razón entre el perímetro del triángulo ABG y el lado AG.

Revisa tu respuesta

Nuevos recursos

Descubrir recursos

Descubre temas