Kümelerde işlemler.2
Fark İşlemi
A ve B herhangi iki küme olsun. A kümesinin elemanları içinden varsa B kümesinin elemanları çıkarılarak elde edilen kümeye “A fark B” kümesi denir ve A \ B ya da A – B şeklinde gösterilir.
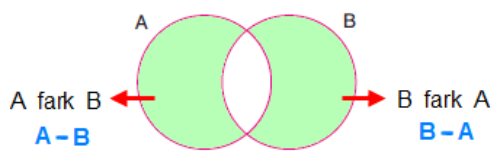
A – A = Ø
E – A = A'
A – B = A ∩ B'
A ? B ise A – B ? B – A
A – Ø = A, Ø – A = Ø
(A – B) ∪ B = A ∪ B
(A – B) – C = A – (B ∪ C)
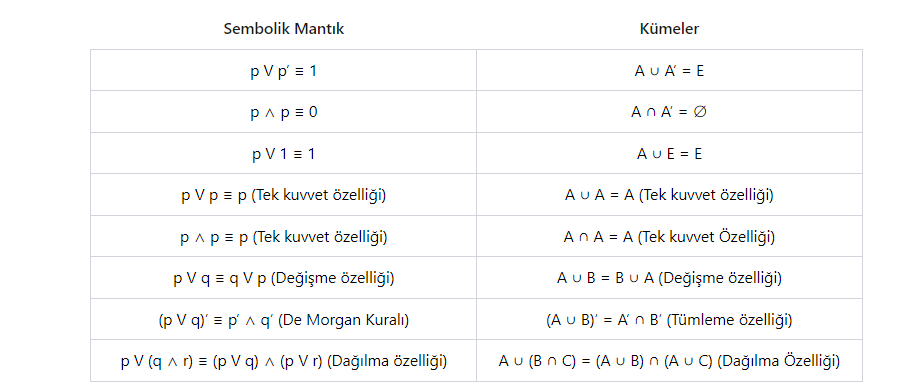
Küme İşlemleri ile Sembolik Mantık Kuralları Arasındaki İlişki
KÜMELERİN ELEMAN SAYISI
A, B, C herhangi birer küme olmak üzere,
Bu iki oyundan hiç birini oynamayanların sayısı:
- s(A È B) = s(A) + s(B) – s(A Ç B)
- s(A È B È C) = s(A) + s(B) + s(C) – s(A Ç B) – s(A Ç C)– s(B Ç C) + s(A Ç B Ç C)
- s(A È B) = s(A – B) + s(A Ç B) + s(B – A)
- a + b + c + d tane öğrencinin bulunduğu bir sınıfta voleybol oynayan öğrencilerin sayısı s(V) =b+c, tenis oynayan öğrencilerin sayısı s(T) = a + b, voleybol ve tenis oynayan öğrencilerin sayısı s(T Ç V) = b olsun.
Bu iki oyundan hiç birini oynamayanların sayısı: