4.1. Conceito de função
Outro exemplo: A quantidade de combustível consumida por um automóvel é função da distância que ele percorre. Nessa afirmação usamos a expressão "depende de" ou “é função de” para mostrar que a quantidade de combustível depende do número de quilômetros ro


Veja na tabela os números ditos pelo professor e as respostas dos alunos:
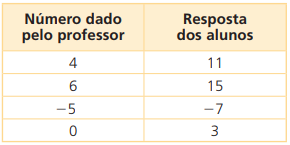
Outro modo de representar essa tabela é por meio de um diagrama:
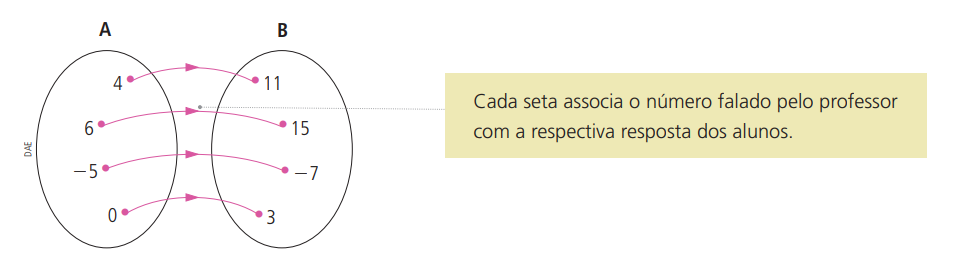
Formamos um conjunto A com os números dados pelo professor e um conjunto B com as respostas dos alunos. Como os conjuntos que relacionamos são A e B, dizemos que essa é uma função de A em B.

Sempre que atribuímos um valor a x e determinamos seu correspondente y por meio da lei de formação da função, obtemos um par de números. Podemos escrever os pares ordenados (x, y) formados no nosso exemplo.
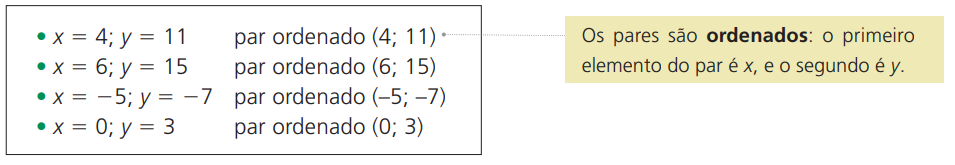
Observe o seguinte exemplo:

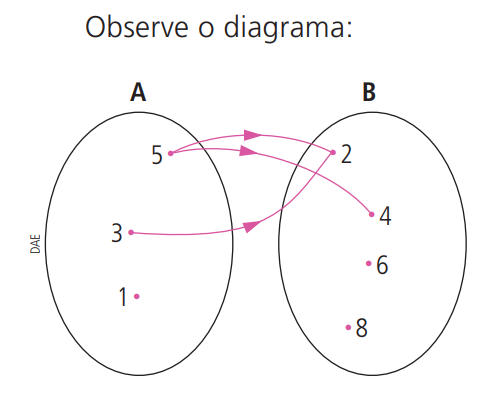
Formamos um conjunto A com os números escolhidos pelo professor e um conjunto B com os números que estavam escritos no quadro. Observe que cada seta faz corresponder o número dado pelo professor com o número (ou os números) registrados no quadro que são menores do que ele. A relação entre o número x escolhido pelo professor e o número y que é a resposta dos alunos pode ser representada por y < x. No entanto, aqui, y não é função de x. Veja por quê: • Para um mesmo valor de x do conjunto A, temos mais do que um correspondente y no conjunto B. • Há um valor de x em A que não tem correspondente y em B No nosso exemplo, para x = 1 em A não temos correspondente y em B. Além disso, x = 5 tem dois correspondentes em B. Por isso, não temos uma função.
