Gleichungen umformen - Unterrichtsplanung
Kurzinformation
- Thema: Gleichungen umformen mit Äquivalenzumformungen
- Schulstufe, Fach: 7. Schulstufe, Mathematik
- Dauer: ca. 2 - 3 Unterrichtseinheiten
- SchülerInnenmaterial: Entweder Jamboard (für den Online-Unterricht) oder ca. 50 Streichholzschachteln (falls der Unterricht in Präsenz stattfindet.
Vorwissen und Voraussetzungen
Die Schülerinnen und Schüler wissen:
- wie einfache lineare Gleichungen aufgestellt werden
- wie lineare Gleichungen mit Elementarumformungsregeln umgeformt werden und gelöst werden können
Lernergebnisse und Kompetenzen
Die Schülerinnen und Schüler können:
- einfache lineare Gleichungen selbst konstruieren
- einfache lineare Gleichungen auf haptischem Weg lösen
- lineare Gleichungen mit Äquivalenzumformungen auflösen
- Umkehraufgaben zu Gleichungen aufstellen und lösen
Unterrichtsablauf
Kurzer Überblick über die einzelnen Aktivitäten:
- Aktivität 1: Gleichungen umformen - haptische Einführung
- Aktivität 2: Konstruieren von Gleichungen
- Aktivität 3: Übersetzen in formale Sprache
- Aktivität 4: Das Klassenzimmer als Museum
- Aktivität 5: Tandemübung
Aktivität 1: Gleichungen umformen - haptische Einführung (10 min)
Für die Einführung werden Streichhölzer und Streichholzschachteln benötigt.
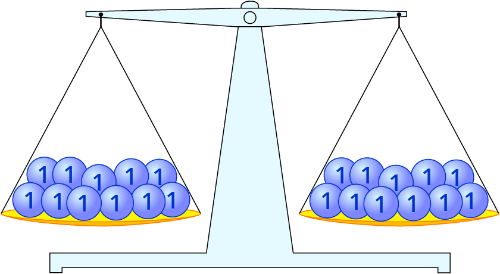
- Die Klasse steht gemeinsam um einen Tisch herum, auf dem eine Balkenwaage steht. Es werden verschiedene Objekte auf die Waage gegeben, um das Prinzip zu veranschaulichen.
- Im Anschluss wird die Waage durch eine Schülerin oder einen Schüler repräsentiert. Eine Freiwillige oder ein Freiwilliger wird zur Waage für Streichhölzer und streckt beide Hände aus.
- Die Lehrperson legt ein Streichholz in die rechte Hand, dadurch geht die rechte Hand etwas nach unten und die linke Hand nach oben. Daraufhin wird in die linke Hand ebenfalls ein Streichholz gegeben --> die Waage ist wieder im Gleichgewicht.
- Besondere Waage --> sie reagiert nur auf Streichhölzer und nicht auf Streichholzschachteln.
- Neues Beispiel: Die Schülerin bzw. der Schüler bekommt acht Streichhölzer in die linke Hand und vier Streichhölzer und zwei Streichholzschachteln in die rechte --> Waage ist im Gleichgewicht.
- Auflösen der Gleichung: auf beiden Seiten der Gleichung werden vier Hölzer entfernt. Danach wird die Menge auf beiden Seiten der Gleichung halbiert --> es befinden sich zwei Hölzer in der linken und eine Schachtel in der rechten Hand.

Aktivität 2 - Konstruieren von Gleichungen (20 min)
In der nächsten Phase wird die Schülerin oder der Schüler, der oder die zuvor die Waage repräsentiert hat, durch einen Stift ersetzt. Es werden nun Gleichungen gemeinsam auf dem Tisch konstruiert.
- Der Stift wird in die Mitte des Tisches gelegt.
- Die Lehrperson fordert eine Schülerin bzw. einen Schüler auf, auf eine Seite des Stiftes 8 bis 12 Streichhölzer zu legen. Um die Waage wieder in ein Gleichgewicht zu bringen muss die selbe Anzahl auch auf die andere Seite gegeben werden.
- Eine weitere Schülerin bzw. ein weiterer Schüler wird aufgefordert 1 bis 3 Streichhölzer, von den Streichhölzern die auf einer Seite der Gleichung liegen, in eine Schachtel zu geben.
- Eine weitere Schülerin bzw. ein weiterer Schüler darf nun mehrere Schachteln auf diese Weise bestücken (in jeder Schachtel müssen sich dann gleich viele Hölzer befinden).
- Nun stellt sich die Frage, wie viele Hölzer in einer Schachteln sind. In diesem Fall ist diese natürlich sehr leicht zu beantworten, da die Schülerinnen und Schüler bei der Konstruktion der Aufgabe dabei waren.
- Im Anschluss stellt die Lehrperson eine neue Aufgabe, die Schülerinnen und Schüler müssen die Augen schließen. Jetzt stellt sich wieder die Frage, wie viele Streichhölzer sich in einer Schachtel befinden, wer die Antwort weiß, verschränkt die Arme. Die Aufgabe wird dann gemeinsam gelöst. Für jeden einzelnen Umformungsschritt wird eine andere Schülerin bzw. ein anderer Schüler ausgewählt.
Aktivität 3: Übersetzen in formale Sprache (20 min)
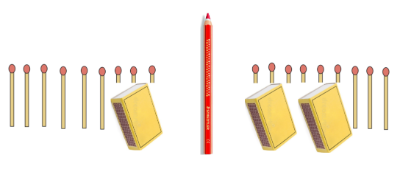
Im Moment gibt es weder Zahlen, noch Variablen oder Gleichheitszeichen, sondern lediglich Hölzer, Schachteln und Waagen. Daher wird die Aufgabe jetzt in eine mathematische Sprache übersetzt. Für eine Schachtel wird nun ein "s" geschrieben, für jedes Hölzchen eine Eins und für den Stift ein Gleichheitszeichen. Das Wort "und" wird als ein "+" dargestellt. Dabei sollte auch klargestellt werden, dass man eine Schachtel und ein Streichholz nicht zusammenzählen kann, da es ja verschiedene Dinge sind.
Ist die Aufgabe in eine Gleichung übersetzt worden, wird die Aufgabe nun von den Schülerinnen und Schülern gemeinsam gelöst. Dabei wird rechts von der Gleichung der Name der Schülerin/des Schülers geschrieben, welche/welcher einen Umformungschritt vorschlägt. Neben den Namen wird
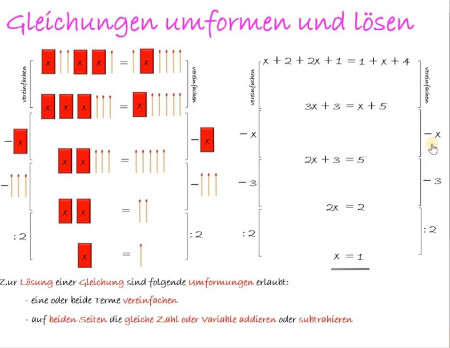
in Worten der Umformungsschritt formuliert und links unter der Gleichung wird dieser in der formalen Sprache durchgeführt. (siehe Tafelbild)

Anschließend werden die erlaubten Äquivalenzumformungen schriftlich im Schulübungsheft festgehalten. Beispielhaft werden dazu drei Aufgaben gelöst. (siehe Tafelbild für den Hefteintrag)

Aktivität 4: Museum der Gleichungen (30 min)
Für diese Aktivität werden ca. 50 Streichholzschachteln benötigt.
Die Schülerinnen und Schüler konstruieren zuerst selbst eine Aufgabe und im Anschluss werden die Gleichungen der anderen zuerst haptisch und dann formal gelöst.
- Konstruktion der Gleichungen: Es werden immer 2er Teams gebildet. Die Gleichungen werden wie in Aktivität 2 konstruiert, wobei auch halbe Hölzer verwendet werden dürfen. Der Tisch wird bis auf die gelegte Gleichung vollständig leer geräumt.
- Haptisches Lösen fremder Aufgaben: Das Klassenzimmer sieht nun aus wie ein Museum voller Gleichungen. Die 2er-Teams gehen nun reihum und versuchen die Aufgaben der anderen zu lösen. Dabei werden die Schachteln und Hölzer nicht entfernt, sondern nur verschoben. Wenn die Aufgabe richtig gelöst wurde, wird die Lösungsmenge kontrolliert und die Gleichung dann wieder in den Originalzustand zurückgebracht. (Je nach Klassengröße müssen die Schülerinnen und Schüler eine bestimmte Anzahl der fremden Gleichungen lösen)
- Übersetzen in formale Sprache: Die Schülerinnen und Schüler müssen sich nun vier Gleichungen aussuchen. Diese müssen sie in ihr Heft zeichnen, um sie anschließend, wie in Aktivität 3, in formale Sprache zu übersetzen und dann formal zu lösen.
- Die Schülerinnen und Schüler werden wieder in 2er-Teams eingeteilt und in Breakout-Rooms geschickt. Die Lernenden müssen sich die Nummer ihres Breakout-Rooms merken, da dies ihre Nummer für ihre Seite im Jamboard ist.
- Auf jeder Seite im Jamboard befinden sich die gleiche Anzahl an virtuellen Streichhölzern und Schachteln. Diese können beliebig gelöscht oder dupliziert werden.
- Die Aufgabe der Schülerinnen und Schüler ist es nun, eine Gleichung zu konstruieren. Dafür entscheidet man sich zuerst, wie viele Streichhölzer auf jeder Seite des Stiftes benötigt werden. Im Anschluss gibt man wieder eine bestimmt Anzahl in eine Schachtel, nur dass diese hier nicht in die Schachtel reingegeben werden, sondern die Schachtel einfach über die Streichhölzer geschoben wird. Wichtig: Die Streichhölzer die sich in der Schachtel "befinden" nicht löschen, da die Aufgabe sonst nicht mehr kontrolliert werden kann.
- Im Anschluss müssen sich die 2er-Teams durch die einzelnen Seiten des Jamboard klicken und die Gleichungen der anderen lösen. Dazu wird die Gleichung, wie in Aktivität 3, auf ein Blatt Papier gezeichnet, in formale Sprache übersetzt und dann gelöst.


Aktivität 5: Tandemübung (20 min)
Ablauf:
- Aufgaben stellen Die Schülerinnen und Schüler bilden Tandems. Sie entwickeln in Einzelarbeit Aufgaben innerhalb eines vorgegebenen Rahmens.
- Tauschen, Bearbeiten, Bewerten Sie tauschen die entwickelten Aufgaben innerhalb der Tandems aus und bearbeiten sie in Einzelarbeit. Danach bewertet jeder die gestellten Aufgaben: Hat die Partnerin, der Partner den Rahmen beim Aufgabenstellen eingehalten?
- Besprechen Die Partner überprüfen gegenseitig ihre Lösungen zu den Aufgaben und diskutieren Unstimmigkeiten, Schwierigkeiten oder Entdeckungen.
- Finde mindestens zwei Gleichungen, die den Tag und den Monat deines Geburtsdatums als Lösung haben. (Wer am 5. November 2007 geboren ist, muss also Gleichungen mit den Lösungen 5 und 11 finden.)
- Tausche deine Gleichungen mit denen deiner Tandempartnerin / deines Tandempartners aus und löse die Gleichungen mit Hilfe von Äquivalenzumformungen. Wann hat er / sie Geburtstag?
- Besprecht anschließend eure Bearbeitungen und helft einander, wo es erforderlich ist. Überlegt zusammen, wie man ganz einfach möglichst viele verschiedene Gleichungen mit derselben Lösung finden kann.
Sicherung / Hausübung
Den Schülerinnen und Schülern wird im Moodle-Kurs der Klasse der Link zum Video "Gleichungen umformen und Lösen" bereitgestellt. So können bestehende Unsicherheiten geklärt werden. Außerdem stellt es eine gute Wiederholung des Unterrichts dar.
Als Hausübung können folgende LearningApps zum Üben aufgegeben werden:
- Wie lautet die Gleichung?
- Welche Äquivalenzumforumung wird hier im Waagenmodell dargestellt?
- Gleichungen lösen mit der Gleichungswaage
Überprüfung des Lernerfolges
Die Überpüfung während der Unterrichtssequenz erfolgt im Rahmen der Tandemübung. Hier sollen die Schülerinnen und Schüler eigenverantwortlich überprüfen, ob sie das gelernte verstanden haben und anwenden können. Ist das nicht der Fall, steht die Tandemparterin, der Tandempartner für Hilfestellungen zur Verfügung. Kann das Problem trotzdem nicht behoben werden, steht eine anschließende Plenumsphase zur Verfügung.
Nach der Unterrichtssequenz sollen die LearningApps eine Überprüfung des Kompetenzerwerbs ermöglichen. Dazu ist allerdings eine Anmeldung auf der Website notwendig.
Links zu Materialien
Quellen
Barzel , B., Büchter, A., & Leuders, T. (2019). Mathematik Methodik. Berlin: Cornelsen Verlag GmbH.
Barzel, B., & Holzäpfel, L. (2011). Gleichungen verstehen. mathematik lehren, S. 2-7.
Kramer, M. (2016). Mathematik als Abenteuer. Band II: Algebra und Vektorrechnung. Seelze: Friedrich Verlag GmbH.
Reichel, H.-C., & Humenberger, H. (Hrsg.). (2009). Das ist Mathematik 3. Wien: Österreichischer Bundesverlag Schulbuch GmbH & Co. KG.
Bild vom Anfang: kapiert.de