BinomialLog
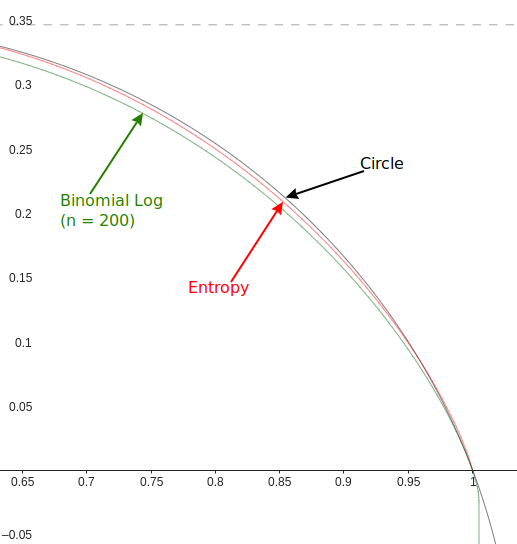
The half of logarithm of binomial coefficient approaches the binary entropy function Hb in base e2, as n approaches infinity, which is very close to an arc of a perfect circle.
Binomial coefficient = = number of k-combinations of n, and beta function B(p, q):
Normalized log of binomial: (x = k/n)
lB approaches Hb in base e as n approaches infinity:
Half of lB approaches Hbs (Hb in base e2) as n approaches infinity:
Hbs (in red) is very close to an arc of circle C (in black):
Distributions
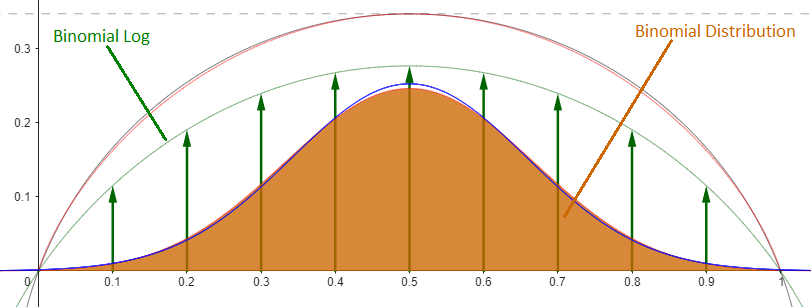
In binomial distribution of a fair coin, X ~ B(n, p=1/2), the probability of getting exactly k heads in n independent Bernoulli trials is the ratio between the number of k-combinations and the total number of combinations 2n:
When n approaches infinity, this distribution approaches the normal distribution N(μ=n/2, σ2=n/4), and its probability mass function Bd(x), normalized by scaling both axes by √n and centering to 1/2, approaches the probability mass function φ(x| μ=0, σ=1/2) of the fair normal distribution N(μ=0, σ2=1/4):
Derivatives
Derivatives of the binary entropy function Hb is related to the logistic map x⋅(1-x):
which is the core form of beta function: